1.

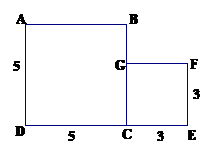
A \(5 × 5\) square and a \(3 × 3\) square can be cut into pieces that will fit together to form a third square.

1. Find the length of a side of the third square.
2. In the diagram below, mark \(P\) on segment \(DC\) so that \(PD = 3\), then draw segments \(PA\) and \(PF\). Calculate the lengths of these segments.
3. Segments \(PA\) and \(PF\) divide the squares into pieces. Arrange the pieces to form the third square.

2.

(Continuation) Change the sizes of the squares to \(AD = 8\) and \(EF = 4\) and redraw the diagram. Where should point \(P\) be marked this time? Form the third square again.

3.

(Continuation) Will the preceding method always produce pieces that form a new square? If your answer is yes, prepare a written explanation. If your answer is no, provide a counterexample – two specific squares that cannot be converted to a single square.

4.

Some terminology: In a right triangle, the legs are the sides adjacent to the right angle. The hypotenuse is the side opposite to the right angle. Given the two points \(A = (3, 7)\) and \(B = (5, 2)\) find \(C\) so that \(\Delta ABC\) is a right triangle with the right angle at \(C\). How long are legs? How long is the hypotenuse?

5.

Let \(A = (0, 0)\), \(B = (7, 1)\), \(C = (12, 6)\), and \(D = (5, 5)\). Plot these points and connect the dots to form the quadrilateral \(ABCD\). Verify that all four sides have the same length. Such a figure is called equilateral.

6.

The main use of the Pythagorean Theorem is to find distances. Originally (6th century BC), however, it was regarded as a statement about areas. Explain this interpretation.

7.

The length of a rectangle is \((3x – 4)\) and the width is \((2x + 1)\). Find the perimeter and area of this rectangle.

8.

Graph the parabola \(y=2x^2-133x+2\) on your graphing calculator.

On a NumWorks calculator or iPad app:

Go into the Grapher application and enter the function.

On a TI-84:

Press the y = button and enter the equation. Press the Graph key. If you are using a TI-84, perform the following steps.

1. What do you see on your screen?
2. Press the Window button (next to y = ), and enter Xmin = −50, Xmax = 50, Xscl = 10, Ymin = −500, Ymax = 500 , Yscl = 100. Press Graph. Now, what do you see?
3. Find a window where you can see the bottom of the curve. Which window did you pick? Present your answer as [Xmin, Xmax], [Ymin, Ymax]. What effect does Xscl and Yscl have on the graph?

9.

Factor: \(x^2-5x+6\)

10.

If the hypotenuse of a right triangle is 12 and one of the legs is 4, express the length of the other leg in simplest radical form.

11.

In the diagram, \(AEB\) is straight and \(\angle A\) and \(\angle B\) are right angles. Calculate the total distance \(DE + EC\).

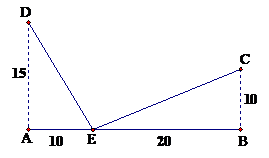
12.

(Continuation) If \(AE = 15\) and \(EB = 15\) instead, would \(DE + EC\) be the same?

13.

CHALLENGE: (Continuation) You have seen that \(DE + EC\) is dependent on the length of \(AE\). Let \(x\) represent \(AE\) (and \(30 − x\) for \(EB\)), write a formula for \(DE + EC\). Enter this formula into your calculator, graph it, and find the value of \(x\) that produces the shortest path from \(D\) to \(C\) through \(E\).

14.

Two different points on the line \(y = 2\) are each exactly 13 units from the point \((7, 14)\). Draw a picture of this situation, and then find the coordinates of these points.

15.

The general notation in geometry is that points are labeled with capital letters and coordinates are defined with lowercase letters. Given the two points \(A\left( {{x_1},{y_1}} \right)\) and \(B\left( {{x_2},{y_2}} \right)\) what do the subscripts on \(x\) and \(y\) represent? If \(\Delta ABC\) is a right triangle with \(C\) being the right angle, find expressions for the lengths of all three sides.

16.

On your calculator or on the Numworks app on your iPad, find the intersection of \(4x + 5y = 8\) and \(y = 0.6x – 4\).

To find the intersection of two lines using a TI-84 calculator, first graph the lines (press Y=) and make sure that you can see the intersection point in the window. If you can't, be sure to change the window accordingly. Then bring up the CALC menu (2ND TRACE) and choose intersect. Using the arrow keys, move the cursor along one of the lines close to the point of intersection and press ENTER. The calculator will prompt you to then press ENTER on the other intersecting line. Then, read the coordinates of the intersection point from the bottom of your screen.

17.

Give an example of a point that is the same distance from \((3, 0)\) as it is from \((7, 0)\). Find lots of examples. Describe the configuration of all such points. How does this configuration relate to the two given points?

18.

Verify that the hexagon formed by \(A = (0, 0)\), \(B = (2, 1)\), \(C = (3, 3)\), \(D = (2, 5)\), \(E = (0, 4)\), and \(F = (−1, 2)\) is equilateral. Is it also equiangular?

19.

Draw a 20-by-20 square \(ABCD\). Mark \(P\) on \(AB\) so that \(AP = 8\), \(Q\) on \(BC\) so that \(BQ = 5\), \(R\) on \(CD\) so that \(CR = 8\), and \(S\) on \(DA\) so that \(DS = 5\). Find the lengths of the sides of quadrilateral \(PQRS\). Is there anything special about this quadrilateral? Explain.

20.

Given the two points \(A = (−2, 1)\) and \(B = (4, 7)\) describe two different methods to find the distance between \(A\) and \(B\). Which method do you prefer?

21.

How would you proceed if you were asked to verify that \(P = (1, −1)\) is the same distance from \(A = (5, 1)\) as it is from \(B = (−1, 3)\)? It is customary to say that \(P\) is equidistant from \(A\) and \(B\). Find three more points that are equidistant from \(A\) and \(B\). By the way, to “find” a point means to find its coordinates. Can points equidistant from \(A\) and \(B\) be found in every quadrant?

22.

CHALLENGE: The two-part diagram below, which shows two different dissections of the same square, was designed to help prove the Pythagorean Theorem. Provide the missing details.

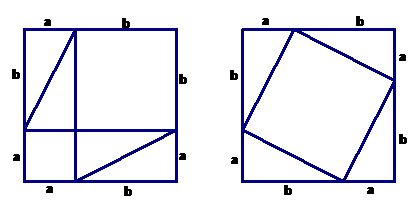
23.

Find both points on the line \(y = 3\) that are 10 units from \((3, −3)\)

24.

On a number line, where is \({\textstyle{1 \over 2}}\left( {p + q} \right)\) in relation to \(p\) and \(q\)?

25.

Some terminology: Figures that have exactly the same shape and size are called congruent. Dissect the region shown below into two congruent parts. How many different ways of doing this can you find?

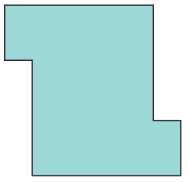
26.

Let \(A = (2, 4)\), \(B = (4, 5)\), \(C = (6, 1)\), \(T = (7, 3)\), \(U = (9, 4)\), and \(V = (11, 0)\). \(\Delta ABC\) and \(\Delta TUV\) are specially related to each other. Make calculations to clarify this statement and write a few words to describe what you discover.

27.

If you were writing a geometry book, and you had to define a mathematical figure called a kite, how would you word your definition?

28.

A triangle that has at least two sides of equal length is called isosceles. Make up an example of an isosceles triangle, one of whose vertices is \((3, 5)\). Give the coordinates of the other two vertices. If you can, find a triangle that does not have any horizontal or vertical sides.

Spreadsheet Lab #1: Pythagorean Theorem and Distance Solver

29.

Let \(A = (1, 5)\) and \(B = (3, −1)\). Verify that \(P = (8, 4)\) is equidistant from \(A\) and \(B\). Find at least two more points that are equidistant from \(A\) and \(B\). Describe all such points.

30.

Solve for \(x\): \(\sqrt {x + 1} = \sqrt {2x - 3} \) . Hint: you can square both sides to eliminate the radical.

31.

Find two points on the y-axis that are 9 units from \((7, 5)\).

32.

A lattice point is a point whose coordinates are integers. For example, \((2, 3)\) is a lattice point, but \((2.5, 3)\) is not. Find two lattice points that are 5 units apart but do not form a horizontal or vertical line.

33.

(Continuation) Find two lattice points that are exactly \(\sqrt {13}\) units apart. Is it possible to find lattice points that are \(\sqrt {15}\) units apart?

34.

Some terminology: When two angles fit together to form a straight angle (a 180° angle, in other words), they are called supplementary angles and either angle is the supplement of the other. When an angle is the same size as its supplement (a 90° angle), it is called a right angle. When two angles fit together to form a right angle, they are called complementary angles and either angle is the complement of the other. Two lines that form a right angle are said to be perpendicular. Draw a diagram for each definition.

35.

Two iron rails, each 50 feet long, are laid end to end with no space between them. During the summer, the heat causes each rail to increase in length by 0.04%. Although this is a small increase, the lack of space at the joint makes the joint buckle upward. What distance upward will the joint be forced to rise? (Assume that each rail remains straight, and that the other ends of the rails are anchored.) Round your answer to the nearest hundredth.

36.

Graph the lines \(2x-y=5\) and \(x+2y=-10\) on a piece of graph paper on the same set of axes. Using your protractor, measure the angle of intersection.

37.

Blair is walking along the edge of her room toward a wall where an Emma bug is crawling along the crown molding (top edge of the wall). Assuming the bug does not change direction, will their paths ever cross? Are their paths parallel?

38.

The point on segment \(AB\) that is equidistant from \(A\) and \(B\) is called the midpoint of \(AB\). For each of the following, find coordinates for the midpoint of \(AB\):

1. \(A = (−1, 5)\) and \(B = (5, −7)\)
2. \(A = (m, n)\) and \(B = (k, l)\)

39.

A unique line exists through any two points. In one form or another, this statement is a fundamental postulate of Euclidean geometry – accepted as true, without proof. Taking this for granted, then, what can be said about three points?

40.

Using GeoGebra, plot the points \(P = (3, 5)\), \(Q = (0, 0)\) and \(R = (−5, 3)\). Measure \(\angle PQR\), being careful to select the points in a clockwise manner. Create the segments \(PQ\) and \(QR\). Use the Slope tool in the same toolbox as the Angle tool to find the slope of segment \(PQ\). Do the same thing for segment \(QR\). Make a conjecture about how these slopes are related. Verify by calculating the slopes by hand.

41.

Write a formula for the distance from \(A = (−1, 5)\) to \(P = (x, y)\), and another formula for the distance from \(P = (x, y)\) to \(B = (5, 2)\). Then write an equation that says that \(P\) is equidistant from \(A\) and \(B\). Simplify your equation to linear form.

42.

(Continuation) The line you just found is called the perpendicular bisector of \(AB\). Verify this by calculating two slopes and one midpoint.

43.

Is it possible to form a square whose area is 18 by connecting four lattice points? Explain.

44.

Find the slope of the line through

1. \((3, 1)\) and \((3 + 4t, 1 + 3t)\);
2. \((m − 5, n)\) and \((5 + m, n^2)\).

45.

Is it possible for a line \(ax + by = c\) to lack a \(y\)-intercept? To lack an \(x\)-intercept? Explain.

46.

Factor:

1. \(x^2-16\)
2. \({x^2} + 8x + 16\)
3. \({x^2} + 6x - 16\)

47.

Find the point of intersection of the lines \(3x + 2y = 1\) and \(-x+y=-2\).

48.

The sides of a triangle are formed by the graphs of \(3x + 2y = 1\), \(y = x − 2\) and \(-4x+9y=22\). Use GeoGebra to discover if the triangle is isosceles. How do you know?

49.

Consider the linear equation \(y = 3.5(x − 1.3) + 2\).

1. What is the slope of this line?
2. What is the value of \(y\) when \(x = 1.3\)?
3. This equation is written in point-slope form. Explain the terminology.
4. Use your calculator or GeoGebra to graph this line.
5. Find an equation for the line through \((4.2, −2.5)\) that is parallel to this line. Leave your answer in point-slope form.
6. Describe how to graph by hand a line that has slope −2 and that goes through the point \((−7, 3)\).

50.

For each of the following questions, fill in the blank with always true (A), never true (N), or sometimes true (S). Please write a few sentences explaining your choice.

1. Two parallel lines are ________ coplanar.
2. Two lines that are not coplanar _______ intersect.
3. Two lines parallel to the same plane are ________ parallel to each other.
4. Two lines parallel to a third line are ________ parallel to each other.
5. Two lines perpendicular to a third line are ________ perpendicular to each other.