back home

GeoGebra Lab 2

In this lab, you will explore the various ways to create circles.

  1. Follow Step A in GeoGebra Lab #1 to remove the axes and set up a blank background. The tools to create circles are in the toolbox with the circle icon. Click it for a drop-down menu of options. Try out the “Circle with Center Through Point” option by following the instructions you see when you hover your mouse over the menu option. Press ESC or select the Select/Move tool (shown at right and labeled D in Lab #1) and move the two points around to see what happens. Is there any way to move the circle that doesn’t change it?
  2. Right-click the circle (not the center or the point on the circle) and notice that this gives you its name and how it was constructed. It also gives you several other options. Rename this circle “Circle_1.” Notice that this creates a subscript.
  3. Now, right-click the circle again and choose Settings. Explore some of the options in the box that pops up. Especially look through the Style and Color tabs.
  4. Try the Circle with Center and Radius tool. How is it different? Name this circle, “Circle_2” and change its color.
  5. Right-click Circle1 and uncheck the box labeled Show Object. Do the same thing for Circle2. This hides the circles. You can do this for any other objects on the screen.

  6. Construct a segment using the line tool (pictured at right and labeled E in Lab #1) and the Segment menu option. Return to the circle tool and choose the Compass option. Click on one endpoint of the segment, then the other endpoint to set the compass radius, then select one of the endpoints of this segment as the center of the circle. Repeat, using the other endpoint of the segment as its center. Your diagram should look like this:

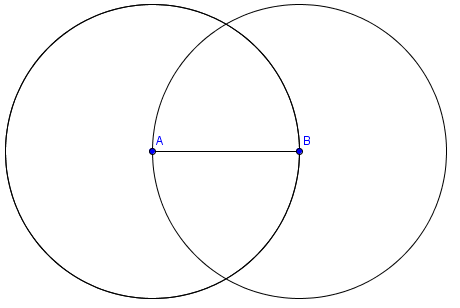
    Two circles that share a radius
  7. Create the intersection points of the two circles using the Intersect tool in the Point toolbox (pictured below). Then, connect these intersections with a line. What do you think is special about this line? Hint: How do the points on the line relate to the endpoints of the segment?
    GeoGebra Intersect tool
  8. Find a way to check your conjecture.
back home