51.

A slope can be considered a rate. Explain this interpretation and give an example.

52.

Given the points $A = (−2, 7)$ and $B = (3, 3)$, find two points $P$ that are on the perpendicular bisector of $AB$. In each case, what can be said about the $\Delta PAB$?

53.

Explain the difference between a line that has undefined slope and a line whose slope is zero.

54.

Three squares are placed next to each other as shown. The vertices $A$, $B$, and $C$ are collinear. Find the dimension $n$.

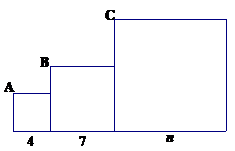
three adjacent squares sides 4, 7, and n

55.

(Continuation) Replace the lengths 4 and 7 by $m$ and $k$, respectively. Express $k$ in terms of $m$ and $n$.

56.

A five-foot tall Emma student casts a shadow that is 40 feet long while standing 200 feet from a streetlight. How high above the ground is the lamp?

57.

(Continuation) How far from the streetlight should the student stand in order to cast a shadow that is exactly as long as the student is tall?

58.

An airplane 27,000 feet above the ground begins descending at the rate of 1501.5 feet per minute. Assuming the plane continues at the same rate of descent, how long will it be before it is on the ground?

59.

(Continuation) Graph the line $y = 27000 – 1501.5x$, using an appropriate window on your calculator. With the preceding problem in mind, explain the significance of the slope of this line and its two intercepts.

60.

In a dream, Blair is confined to a coordinate plane, moving along a line with a constant speed. Blair’s position at 4:00 am is $(2, 5)$ and at 6:00 am it is $(6, 3)$. What is Blair’s position at 8:15 am when the alarm goes off?

61.

Find a way to show that points $A = (−4, −1)$, $B = (4, 3)$, and $C = (8, 5)$ are collinear.

62.

Find as many ways as you can to dissect each figure below into two congruent parts.

63.

An airplane is flying at 36,000 feet directly above Lincoln, Nebraska. A little later the plane is flying at 28,000 feet directly above Des Moines, Iowa, which is 160 miles from Lincoln. Assuming a constant rate of descent, predict how far from Des Moines the airplane will be when it lands.

64.

Is there enough evidence in the given diagram below to conclude that the triangle is right? Explain why or why not?

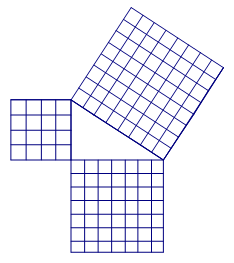
65.

Golf balls cost $0.90 each at Emma’s Club, which has an annual $25 membership fee. At Wendy & Marilyn’s sporting goods store, the price is $1.35 per ball for the same brand. Where you buy your golf balls depends on how many you wish to buy. Explain, and illustrate your reasoning by drawing a graph.

Spreadsheet Lab #2: Line Calculator

66.

CHALLENGE: Let $P = (a, b)$, $Q = (0, 0)$, and $R = (−b, a)$, where $a$ and $b$ are positive numbers. Prove that $\angle PQR$ is right, by introducing two congruent right triangles into your diagram by connecting points $P$ and $R$ to the $x$-axis. Using these two triangles, verify that the slope of segment $QP$ is the opposite reciprocal of the slope of segment $QR$.

67.

Draw the following segments. What do they have in common?

From $(3, −1)$ to $(10, 3)$;
From $(1.3, 0.8)$ to $(8.3, 4.8)$;
From $(\sqrt 3 ,\sqrt 2 )$ to $(7 + \sqrt 3, 4 + \sqrt 2)$

68.

(Continuation) The above segments all have the same length and the same direction. Each represents the vector $[7, 4]$. The horizontal component of the vector is positive 7 and the vertical component is positive 4.

Find another example of two points that represent this vector. The initial point of your segment is called the tail of the vector, and the final point is called the head.
Which of the following segments represents vector [7, 4]?
1. from $(−2, −3)$ to $(5, −1)$
2. from $(−3, −2)$ to $(11, 6)$
3. from $(10, 5)$ to $(3, 1)$
4. from $(−7, −4)$ to $(0, 0)$

69.

Given the line $y = {\textstyle{3 \over 4}}\left( {x + 3} \right) - 2$ and the point $(9, 2)$. Using point-slope form, write equations for the lines parallel and perpendicular to this line through the given point.

70.

Show that the triangle formed by the lines $y = 2x − 7$, $x + 2y = 16$, and $3x + y = 13$ is isosceles. Show also that the lengths of the sides of this triangle fit the Pythagorean theorem. Can you identify the right angle just by looking at the equations?

71.

The perimeter of an isosceles right triangle is 24 cm. How long are its sides?

Geogebra Lab #5.

GeoGebra Lab #5

72.

A triangular plot of land has boundary lines of 45 meters, 60 meters, and 70 meters. The 60-meter boundary runs north-south. Is there a boundary line for the property that runs due east-west?

73.

Using GeoGebra, plot the points $A = (−5, 0)$, $B = (5, 0)$, and $C = (2, 6)$, then the points $K = (5, −2)$, $L = (13, 4)$, and $M = (7, 7)$. Find the lengths of each side and the measure of each angle of the $\Delta ABC$ and $\Delta KLM$. It is customary to call two triangles congruent when all corresponding sides and angles are the same.

74.

(Continuation) Are the triangles related by a vector translation? Why?

75.

Let $A = (1, 2)$, $B = (5, 1)$, $C = (6, 3)$, and $D = (2, 5)$. Let $P = (−1, −1)$, $Q = (3, −2)$, $R = (4, 0)$, and $S = (0, 2)$. Use a vector to describe how quadrilateral $ABCD$ is related to quadrilateral $PQRS$. What is the length of this vector?

76.

Let $K = (3, 8)$, $L = (7, 5)$, and $M = (4, 1)$. Find coordinates for the vertices of the triangle that is obtained by sliding $\Delta KLM$ two units to the right and five units down. How far does each vertex slide?

77.

The length of a vector is defined as the hypotenuse of the right triangle created by its components. The horizontal component of the vector $[−1, 7]$ is −1 and the vertical component is 7. What is the length of the vector $[−1, 7]$? What is the length of vector $[a, b]$? Some notation: the length of a vector is written as $\left| {\left[ {a,b} \right]} \right|$.

78.

Let $A = (2, 4)$, $B = (4, 5)$, and $C = (6, 1)$. Draw three new triangles as follows:

$\Delta PQR$ has $P = (11, 1)$, $Q = (10, −1)$, and $R = (6, 1)$;
$\Delta KLM$ has $K = (8, 10)$, $L = (7, 8)$, and $M = (11, 6)$;
$\Delta TUV$ has $T = (2, 7)$, $U = (0, 8)$, and $V = (−2, 4)$.

These triangles are not obtained from $\Delta ABC$ by applying a translation. Instead, each of the appropriate transformations is described by one of the suggestive names reflection, rotation, or glide-reflection. Decide which is which, with justification.

79.

The juniors are jealous of the seniors and they want to copy the senior triangle onto the lacrosse field. They have a limited amount of time, so they measure one of the sides and create a congruent segment on the field. If they do not do any more measurements does this guarantee that the junior triangle will be congruent to the senior triangle? Sketch a diagram of this scenario. Another group measured only one angle and created a congruent angle on the field. If they do not do any more measurements does this guarantee that the junior triangle will be congruent to the senior triangle? Sketch a diagram.

80.

In baseball, the bases are placed at the corners of a square whose sides are 90 feet long. Home plate and second base are at opposite corners. How far is it from home plate to second base to two decimal places?

81.

Give the components of the vector whose length is 10 and that points in the opposite direction of $[−4, 3]$.

82.

A 9-by-12 rectangular picture is framed by a border of uniform width. Given that the combined area of picture plus frame is 180 square units, find the width of the border.

83.

Let $A = (0, 0)$, $B = (2, −1)$, $C = (−1, 3)$, $P = (8, 2)$, $Q = (10, 3)$, and $R = (5, 3)$. Plot these points. $\angle BAC$ and $\angle QPR$ should look like they are the same size. Find evidence to support this conclusion.

84.

The juniors realize that copying a single measurement will not guarantee an exact copy of the senior triangle. They decide to try measuring two parts. What are the combinations of two corresponding parts that they could measure? Does the use of any of these pairs ensure congruent triangles?

85.

An equilateral quadrilateral is called a rhombus. A square is a simple example of a rhombus. Find a non-square rhombus whose diagonals and sides are not parallel to the rulings on your graph paper. Use coordinates to describe its vertices. Write a brief description of the process you used to find your example.

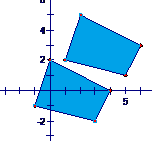
86.

CHALLENGE: Compare the two figures shown below. Is there anything wrong with what you see? Write a few sentences justifying your answer.

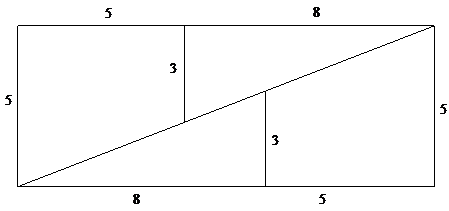
87.

A bug is initially at $(−3, 7)$. Where is the bug after being displaced by vector $[−7, 8]$?

88.

Plot points $K = (0, 0)$, $L = (7, −1)$, $M = (9, 3)$, $P = (6, 7)$, $Q = (10, 5)$, and $R = (1, 2)$. Show that $\Delta KLM \cong \Delta RPQ$ (that the triangles are congruent). Show also that neither triangle is a vector translation of the other. Describe how one triangle has been transformed into the other.

89.

What is the slope of the line $ax + by = c$? Find an equation for the line through the origin that is perpendicular to the line $ax + by = c$.

90.

Let $A = (3, 2)$ and $B = (7, −10)$. What is the displacement vector that moves point $A$ onto point $B$? What vector moves $B$ onto $A$?

91.

Realizing that one or two corresponding parts do not ensure congruent triangles the juniors’ conjecture that they must use three parts to create a new junior triangle. Create a table of the possibilities. Which do you think will work and why?

92.

CLASS PROBLEM: Access a GeoGebra sketch called Triangle Congruence Criteria. You will be told in class where to find it. Explore this sketch. Do any of the scenarios confirm or contradict your conjectures?

Geogebra Lab #6

93.

Choose a point $P$ on the line $2x + 3y = 7$, and draw the vector $[2, 3]$ with its tail at $P$ and its head at $Q$. Confirm that the vector is perpendicular to the line. What is the distance from $Q$ to the line? Repeat the preceding, with a different choice for point $P$.

94.

We know that $|[3,4]|=5$; how do we find a vector that points in the same direction and has length 1? We call a vector of length 1 a unit vector.

95.

Let $M = (a, b)$, $N = (c, d)$, $M' = (a + h, b + k)$, and $N' = (c + h, d + k)$. Use the distance formula to show that segments $MN$ and $M'N'$ have the same length. Explain why this could be expected.

96.

Some terminology: When the components of the vector $[5, −7]$ are multiplied by a given number $t$, the result may be written either as $[5t, −7t]$ or as $t[5, −7]$. This is called the scalar multiple of vector $[5, −7]$ by the scalar $t$. Find components for the following scalar multiples:

$\left[ {12,-3} \right]$ by scalar 5
$\left[{\sqrt 5, \sqrt {10}}\right]$ by scalar $\sqrt 5$
$\left[{ - {\textstyle{3 \over 4}} , {\textstyle{2 \over 3}}}\right]$ by scalar $ - {\textstyle{1 \over 2}} + {\textstyle{2 \over 6}}$
$\left[ {p, q}\right]$ by scalar $\frac{1}{{pq}}$

97.

If two figures are congruent, then their parts correspond. In other words, each part of one figure has been matched with a definite part of the other figure. Given congruent triangles $\Delta KLM$ and $\Delta RPQ$, in the triangle $\Delta RPQ$, which angle corresponds to $\angle M$? Which side corresponds to $KL$? In general, what can be said about corresponding parts of congruent figures? How might you confirm your hunch experimentally?

98.

A nice acronym to shorten the statement about corresponding parts of congruent triangles can be written as CPCTC. What do you think these letters represent?

99.

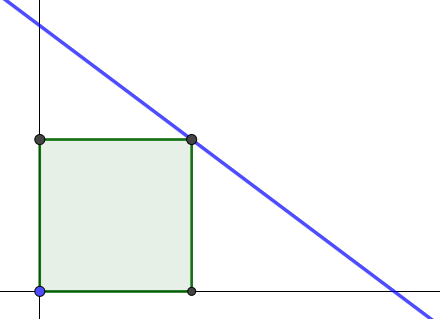
The diagram below shows the graph of $3x + 4y = 12$. The shaded figure is a square, three of whose vertices are on the coordinate axes. The fourth vertex is on the line. Find

the $x$- and $y$-intercepts of the line;
the length of a side of the square.
Show that the fourth vertex is equidistant from the coordinate axes.

100.

Given the vector $[−5, 12]$, find the following vectors:

same direction, twice as long
same direction, length 1
opposite direction, length 10
opposite direction, length $c$