Glossary of Terms
A
- AA similarity
- Two triangles are sure to be similar if at least two of their angles are equal in size.
- adjacent angles
- Two angles with a common vertex that share a side but have no common interior points.
- altitude
- In a triangle, an altitude is a line through one of the vertices, perpendicular to the opposite side. In obtuse triangles, it may be necessary to extend a side to meet the altitude. The distance from the vertex to the point of intersection with the line containing the opposite side is also called an altitude, as is the distance that separates the parallel sides of a trapezoid.
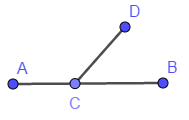
- angle
The figure formed by two rays that share an endpoint called the vertex. Angles can often be identified by a single letter--the point at the vertex--but sometimes three letters are necessary. The angles shown can be called \(\angle ACD\), or \(\angle BCD\) where the middle letter is the vertex.
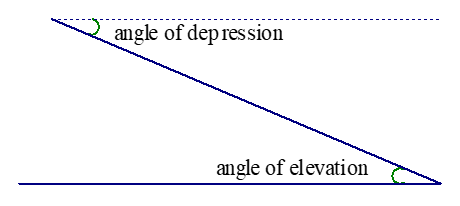
- angle of depression
- Angle formed by a horizontal ray and a line-of-sight ray that is below the horizontal. See the diagram.
- angle of elevation
Angle formed by a horizontal ray and a line-of-sight ray that is above the horizontal. See the diagram.
- Angle-Angle-Side
- When the parts of one triangle can be matched with the parts of another triangle, so that two pairs of corresponding angles have the same sizes, and so that one pair of corresponding sides has the same length, then the triangles are congruent. This rule of evidence is abbreviated as AAS.
- angle bisector
- An angle bisector is a ray that divides the given angle into two equal parts.
- Angle Bisector Theorem
- The bisector of any angle of a triangle cuts the opposite side into segments whose lengths are proportional to the sides that form the angle.
- Angle-Side-Angle
- When the parts of one triangle can be matched with the parts of another triangle, so that two pairs of corresponding angles have the same sizes, and so that the (corresponding) shared sides have the same length, then the triangles are congruent. This rule of evidence is abbreviated as ASA.
- angular size of an arc
- This is the size of the central angle formed by the radii that meet the endpoints of the arc. Also called the measure of the arc.
- arc
- A section of the perimeter of a circle. Can be a minor arc (measure less than 180°) or major arc (measure greater than 180°). The portion of a circle that lies to one side of a chord is also called an arc.
- arc length
- The linear distance along the circle from one endpoint of the arc to the other. Given a circle, the length of any arc is proportional to the size of its central angle.
- areas of similar figures
- If two figures are similar, then the ratio of their areas equals the square of the ratio of similarity.
B
- base
- The base of a triangle is the side that is perpendicular to the altitude. In an isosceles triangle, it refers to the side that is not one of the congruent sides. The base of a pyramid or cone is the face that does not touch the vertex.
- bisect
- Divide into two equal parts.
C
- central angle
- An angle formed by two radii of a circle.
- centroid
- The medians of a triangle are concurrent at this point, which is the balance point (also known as the center of gravity) of the triangle.
- centroid theorem
- The centroid of a triangle is 2/3 of the distance from each vertex to the midpoint of the opposite side.
- chord
A segment that joins two points on a circle is called a chord of the circle.
- circle
- The set of all points equidistant from a given point, called the center. The common distance is the radius of the circle. A segment joining the center to a point on the circle is also called a radius.
- circumcenter
- The perpendicular bisectors of the sides of a triangle are concurrent at this point, which is equidistant from the vertices of the triangle.
- circumscribed circle
- When possible, the circle that goes through all the vertices of a polygon.
- collinear
- Three (or more) points that all lie on a single line are collinear.
- complementary
- Two angles that fit together to form a right angle are called complementary. Each angle is the complement of the other.
- components
- the two parts of a vector that describe how to move from one point to another. Vectors [x, y] describe the motion with the x component (describing the horizontal shift) and the y component (the vertical shift). They are obtained by subtracting coordinates, being mindful of the direction of the vector.
- concentric
- Two figures that have the same center are called concentric.
- concurrent
- Three (or more) lines that go through a common point are concurrent.
- concyclic
- Points that all lie on a single circle are called concyclic.
- congruent
- When the points of one figure can be matched with the points of another figure, so that corresponding parts have the same size, then the figures are called congruent, which means that they are considered to be equivalent.
- converse
- The converse of a statement of the form"if [something] then [something else]” is the statement"if [something else] then [something].”
- convex
- A polygon is called convex if every segment joining a pair of points within it lies entirely within the polygon.
- coordinates
- Numbers that describe the position of a point in relation to the origin of a coordinate system.
- corresponding
- They are parts of polygons that are in the same position relative to each other. Corresponding describes parts of figures (such as angles or segments) that could be matched by means of a transformation. In congruent polygons, if the polygons were superimposed, the corresponding parts would be right on top of one another.
- cosine ratio
- Given a right triangle, the cosine of one of the acute angles is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. The word cosine is a combination of complement and sine, so named because the cosine of an angle is the same as the sine of the complementary angle.
- CPCTC
- Corresponding Parts of Congruent Triangles are Congruent.
- cyclic
- A polygon, all of whose vertices lie on the same circle, is called cyclic. Also called an inscribed polygon.
D
- decagon
- A polygon that has ten sides.
- diagonal
- A segment that connects two nonadjacent vertices of a polygon.
- diameter
- A chord that goes through the center of a circle is called a diameter.
- dilation
- A similarity transformation, with the special property that all lines obtained by joining points to their images are concurrent at the same central point.
- distance formula
- The distance from \((x_1,y_1 )\) to \((x_2,y_2 )\) is \(\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \). This formula is a consequence of the Pythagorean Theorem.
- dodecagon
- A polygon that has twelve sides.
E
- equiangular
- A polygon all of whose angles are the same size.
- equidistant
- Equally distant. For example, two points are equidistant to a line if they are both the same distance from the line.
- equilateral
- A polygon whose sides have the same length.
- Euclidean geometry
- (also known as plane geometry) is characterized by its parallel postulate, which states that, given a line, exactly one line can be drawn parallel to it through a point not on the given line. A more familiar version of this assumption states that the sum of the angles of a triangle is a straight angle.
- Euler line
- The centroid, the circumcenter, and the orthocenter of any triangle are collinear.
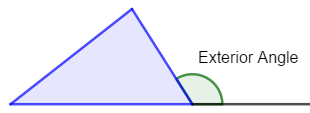
- exterior angle
An angle that is formed by a side of a polygon and the extension of an adjacent side. It is supplementary to the adjacent interior angle.
- Exterior Angle Theorem
- An exterior angle of a triangle is the sum of the two nonadjacent interior angles.
F
G
- glide-reflection
- A transformation created by a vector translation and reflection. The mirror line contains the transformation vector.
- Greek Letters
- Greek letters appear often in mathematics. Some of the common ones are α (alpha), β (beta), Δ or δ (delta), θ (theta), Λ and λ(lambda), μ (mu), π (pi), and Ω or ω (omega).
H
- head
- Vector terminology for the second vertex of a directed segment.
- hexagon
- a polygon that has six sides.
- Hypotenuse-Leg
- When the hypotenuses of two right triangles have the same length, and a leg of one triangle has the same length as a leg of the other, then the triangles are congruent. This rule of evidence is abbreviated as HL.
I
- image
- The result of applying a transformation to a point \(P\) is called the image of \(P\), often denoted \(P'\). One occasionally refers to an image segment or an image triangle.
- incenter
- The angle bisectors of a triangle are concurrent at this point, which is equidistant from the sides of the triangle.
- included angle
- The angle formed by two designated segments.
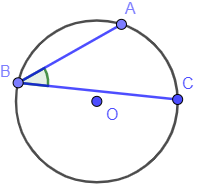
- inscribed angle
An angle formed when two chords meet at a point on the circle. An inscribed angle is half the angular size of the arc it intercepts. An inscribed angle that intercepts a semicircle is a right angle.
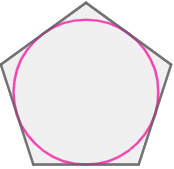
- inscribed circle
The largest circle that can be drawn inside a polygon. The inscribed circle must touch each side of the polygon at exactly one point.
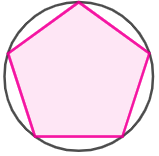
- inscribed polygon
A polygon whose vertices all lie on the same circle; also called a cyclic polygon.
- integer
- Any whole number, whether it be positive, negative, or zero.
- intercepted arc
- The part of an arc that is found inside a given angle.
- isosceles triangle
- A triangle that has two sides of the same length. The word is derived from the Greek iso + skelos (equal + leg)
- Isosceles Triangle Theorem
- If a triangle has at least two sides of equal length, then the angles opposite the congruent sides are also the same size.
- isosceles trapezoid
- A trapezoid whose nonparallel sides have the same length.
K
- kite
- A quadrilateral that has two pairs of congruent adjacent sides.
L
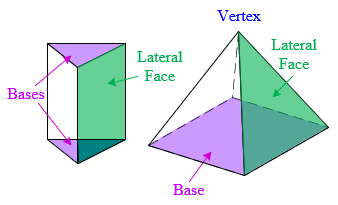
- lateral face
Any face of a pyramid or prism that is not a base.
- lattice point
- A point whose coordinates are both integers.
- lattice rectangle
- A rectangle whose vertices are all lattice points.
- leg
- The perpendicular sides of a right triangle are called its legs.
- length of a vector
- This is the length of any segment that represents the vector. Notation: length of \(\vec v\) is labeled as \(\left| {\vec v} \right|\). if \({\vec v} =[x,y]\), then \(\left| {\vec v} \right| = \sqrt {{x^2} + {y^2}} \).
- linear equation
- Any straight line can be described by an equation in the form \(Ax + By = C\).
- linear pair
- Two adjacent angles whose sum is 180°; Two angles that form a straight angle.
M
- major/minor arc
- A non-diameter chord of a circle divides a circle into two parts. Of the two arcs, the smaller one is called minor (less than 180°), and the larger one is called major (more than 180°). Often, a major arc is described with a label that has 3 letters and a minor arc is described with 2 letters.
- median of a triangle
A segment that joins a vertex of a triangle to the midpoint of the opposite side.
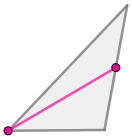
- midsegment
A segment that joins the midpoints of two sides of a triangle.
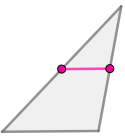
- Midsegment Theorem
- A segment that joins the midpoints of two sides of a triangle is parallel to the third side and is half as long.
- midpoint
- The point on a segment that is equidistant from the endpoints of the segment. If the endpoints are \((a, b)\) and \((c, d)\), the midpoint is \(\left( {{\textstyle{{a + c} \over 2}},{\textstyle{{b + d} \over 2}}} \right)\).
- Mirror line
- In a reflection, the mirror line is the perpendicular bisector of the segments that connect the initial point (pre-image) and its reflected point (image).
N
- Negative (opposite) reciprocal
- One number is the negative reciprocal of another if the product of the two numbers is −1.
O
- octagon
- a polygon that has eight sides.
- opposite
- Two numbers or vectors are opposite if they differ in sign. For example, 17.5 is the opposite of −17.5, and \([2 , −11]\) is the opposite of \([−2, 11]\).
- orthocenter
- The altitudes of a triangle are concurrent at this point.
P
- parallel
- Coplanar lines that do not intersect. When drawn in a coordinate plane, they are found to have the same slope, or else no slope at all. The shorthand // is often used.
- parallelogram
- A quadrilateral that has two pairs of parallel sides.
- pentagon
- a polygon that has five sides.
- perpendicular
- Coplanar lines that intersect to form a right angle.
- perpendicular bisector
- Given a line segment, this is the line that is perpendicular to the segment and that goes through its midpoint. The points on this line are all equidistant from the endpoints of the segment.
- point-slope form
- A non-vertical straight line can be described by \(y - {y_0} = m\left( {x - {x_0}} \right)\) or by \(y = m\left( {x - {x_0}} \right) + {y_0} \). One of the points on the line is \((x_0,y_0)\) and the slope is \(m\).
- postulate
- A statement that is accepted as true, without proof.
- pre-image
- The original geometric object before a transformation is applied to it. (see image)
- prism
- A three-dimensional figure that has two congruent and parallel bases, and parallelograms for its remaining lateral faces. If the lateral faces are all rectangles, the prism is a right prism. If the base is a regular polygon, the prism is also called regular.
- proportion
- An equation that expresses the equality of two ratios.
- pyramid
- A three-dimensional figure that is obtained by joining all the points of a polygonal base to a vertex. Thus, all the lateral faces of a pyramid are triangles. If the base polygon is regular, and the lateral edges are all congruent, then the pyramid is called regular.
- Pythagorean Theorem
- The area of the square with a side equal to the hypotenuse of a right triangle equals the sum of the areas of the squares whose sides are the lengths of the legs of the right triangle. If a and b are the lengths of the legs of a right triangle, and if c is the length of the hypotenuse, then these lengths fit the Pythagorean equation \(a^2 + b^2 = c^2\).
Q
- quadrant
- one of the four regions formed by the coordinate axes. Quadrant I is where both coordinates are positive, and the other quadrants are numbered (using Roman numerals) in a counterclockwise fashion.
- quadratic formula
- \(x = \frac{{ - b + \sqrt {{b^2} - 4ac} }}{{2a}}\) and \(x = \frac{{ - b - \sqrt {{b^2} - 4ac} }}{{2a}}\) are the two solutions to \(ax^2 + bx + c = 0\).
- quadrilateral
- a four-sided polygon.
R
- ratio of similarity
- The ratio of the lengths of any two corresponding segments of similar figures.
- ray
- A ray is a line bounded at one end and infinite at the other.
- rectangle
- An equiangular quadrilateral.
- reflection
- A reflection maps points on one side of the mirror line to the other side. If the point is on the mirror line, then it maps onto itself.
- regular
- A polygon that is both equilateral and equiangular.
- rhombus
- An equilateral quadrilateral.
- right angle
- An angle that is its own supplement, in other words, an angle that is 90°.
- rotation
- A transformation in a plane that moves a figure about a single fixed point. The fixed point is called the center of rotation.
S
- SAS similarity
- Two triangles are certain to be similar if two sides of one triangle are proportional to two sides of the other, and if the included angles are equal in size.
- scalar
- In the context of vectors, this is just another name for a number that can change the magnitude and/or direction of the vector.
- scale factor of a dilation
- The ratio of the length of a dilated segment to its original length. The scale factor can also be defined in terms of distances from the center of dilation. It is the distance to the image of a point divided by the distance to the original point.
- scalene
- A triangle that has 3 different side lengths.
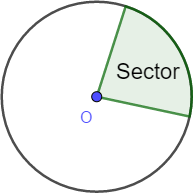
- sector
The region formed by two radii and an arc of a circle.
- segment
- That part of a line that lies between two designated points.
- Sentry Theorem
- The sum of the exterior angles (one per vertex) of any polygon is 360°.
- Side-Angle-Side
- When the parts of one triangle can be matched with the parts of another triangle, so that two pairs of corresponding sides have the same lengths, and so that the (corresponding) angles they form are also the same size, then the triangles are congruent. This rule of evidence is abbreviated as SAS.
- Side-Side-Angle
- Insufficient grounds for congruence. See Hypotenuse-Leg, however.
- Side-Side-Side
- When the parts of one triangle can be matched with the parts of another triangle, so that all three pairs of corresponding sides have the same lengths, then the triangles are congruent. This rule of evidence is abbreviated as SSS.
- similar
- Two figures are similar if their points can be matched in such a way that all ratios of corresponding lengths are proportional to a fixed ratio of similarity. Corresponding angles of similar figures must be equal in size.
- simplest radical form
- A square root expression is in simplest radical form if the number under the radical (the square root sign) is not divisible by a perfect square other than 1. For example, \(\sqrt {18}\) can be written as \(\sqrt {9 \cdot 2} = \sqrt 9 \sqrt 2 = 3\sqrt 2 \).
- sine ratio
- Given a right triangle, the sine of one of the acute angles is the ratio of the length of the side opposite the angle to the length of the hypotenuse.
- skew lines
- Non-coplanar lines that do not intersect.
- slant height
The distance from the vertex of a square pyramid to the midpoint of a base edge. It is the height of one triangle that makes up a lateral face of a square pyramid.

- slope
- The slope of the segment that joins the points \((x_1,y_1)\) and \((x_2,y_2)\) is \({\textstyle{{{y_2} - {y_1}} \over {{x_2} - {x_1}}}}\).
- slope-intercept form
- Any non-vertical straight line can be described by an equation that takes the form \(y = mx + b\). The slope of the line is \(m\), and the y-intercept is \(b\).
- SSS similarity
- Two triangles are similar if their corresponding sides are proportional.
- square
- A regular quadrilateral.
- straight angle
- A 180° angle.
- supplementary
- Two angles whose measures add up to 180° and could be fit together to form a straight line are called supplementary. Each angle is the supplement of the other.
T
- tail
- Vector terminology for the first vertex of a directed segment.
- tail-to-tail
- Vector terminology for directed segments with a common first vertex.
- tangent ratio
- Given a right triangle, the tangent of one of the acute angles is the ratio of the side opposite the angle to the side adjacent to the angle.
- tangent and slope
- When an angle is formed by the x-axis and a ray through the origin, the tangent of the angle is the slope of the ray. Angles are measured in a counterclockwise sense, so that rays in the second and fourth quadrants determine negative tangent values.
- tangent to a circle
- A line that has one and only one intersection with a circle. This intersection is called the point of tangency. Such a line is perpendicular to the radius drawn to the point of tangency.
- tesselate
- To fit non-overlapping tiles together to cover a planar region.
- Three Parallels Theorem
- Given three parallel lines, the segments they intercept on one transversal are proportional to the segments they intercept on any transversal.
- transformation
- A function that maps points to points.
- translation
- A transformation that slides each point of a figure the same distance and same direction by applying a vector to each of its points.
- transversal
- A line that intersects two other lines in a diagram.
- trapezoid
- A quadrilateral with exactly one pair of parallel sides. If the non-parallel sides have the same length, the trapezoid is called isosceles.
- triangle inequality
- The sum of the lengths of two sides of a triangle is greater than the length of the third side.
- two-column proof
A way of outlining a geometric deduction. Steps are in the left column, and supporting reasons are in the right column.
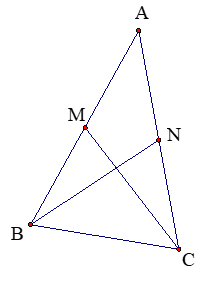
- For example, here is how one might show that an isosceles \(\Delta ABC\) has two medians of the same length. It is given that \(AB = AC\) and that \(M\) and \(N\) are the midpoints of sides \(AB\) and \(AC\), respectively. The desired conclusion is that medians \(CM\) and \(BN\) have the same length.
Statement Reason \(AB = AC\) given \(AM = AN\) \(M\) and \(N\) are midpoints \(\angle MAC \cong \angle NAB\) shared angle \(\Delta MAC \cong \Delta NAB\) SAS \(CM = BN\) CPCTC - Two Tangent Theorem
- From a point outside a circle, there are two segments that can be drawn tangent to the circle. These segments have the same length.
U
- unit circle
- This circle consists of all points that are 1 unit from the origin, \(O\), of the xy-plane. Given a point \(P\) on this circle, the coordinates of \(P\) are the cosine and the sine of the counterclockwise angle formed by segment \(OP\) and the positive x-axis.
V
- vectors
- Vectors have magnitude (size or length) and direction. Visualize vectors as arrows where the length of the arrow is the vector’s magnitude, and the direction of the arrow is the vector’s direction. Vectors are described by components, just as points are described by coordinates. The vector from point \(A\) to point \(B\) is often denoted \(\vec {AB}\) or abbreviated by a boldface letter such as u, and its magnitude is often denoted \(\left| {\vec v} \right|\) or\(\left| {u} \right|\). See Components.
- vertex
- A labeled point in a figure. The plural is vertices. The point on a parabola that is closest to the focus is also called the vertex.
- vertical angles
- Two non-adjacent angles that share a vertex and are formed by the intersection of two lines.
- volume of a prism
- This is the product of the base area and the height, which is the distance between the parallel base planes.
- volume of a pyramid
- This is one third of the product of the base area and the height, which is the distance from the vertex to the base plane.
- volumes of similar figures
- If two three-dimensional figures are similar, then the ratio of their volumes equals the cube of the ratio of similarity.