101.

One of the legs of a right triangle is twice as long as the other and the perimeter of the triangle is 28. Find the lengths of all three sides, to three decimal places.

102.

Find the lengths of the following vectors:

1. \([3, 4]\)
2. \(2006 [3, 4]\)
3. \({ - {\textstyle{2008 \over 5}}}[3,4]\)
4. \(t[3, 4]\)
5. \(t[a, b]\) in terms of \(a\) and \(b\):

103.

A triangle has six principal parts – three sides and three angles. The SSS criterion states that three of these items (the sides) determine the other three (the angles). What other combinations of three parts determine the remaining three? In other words, if the class is given three measurements with which to draw and cut out a triangle, which three measurements will guarantee that everyone’s triangles will be congruent?

104.

The vector that is defined by a segment \(AB\) is often denoted \(\overrightarrow {AB} \). Given \(A(1, 1)\) and \(B(3, 5)\);

1. Use the midpoint formula to find the midpoint of \(AB\) ;
2. Find the vector \(\overrightarrow {AB} \) and multiply by \(\textstyle{1 \over 2}\).
3. Translate \(A\) by \(\textstyle{1 \over 2}\overrightarrow {AB} \). Did you expect this result?

105.

Let \(A = (1, 4)\), \(B = (0, −9)\), \(C = (7, 2)\), and \(D = (6, 9)\). Prove that \(\angle DAB\) and \(\angle DCB\) are the same size. Can anything be said about the \(\angle ABC\) and \(\angle ADC\)?

106.

Plot the three points \(P = (1, 3)\), \(Q = (5, 6)\), and \(R = (11.4, 10.8)\). Verify that \(PQ = 5\), \(QR = 8\), and \(PR = 13\). What is special about these points?

107.

Sydney calculated three distances of the collinear points \(A\), \(B\), and \(C\). She reported them as \(AB = 29\), \(BC = 23\), and \(AC = 54\). What do you think of Sydney’s data, and why?

108.

Find the number that is two thirds of the way (a) from −7 to 17; (b) from \(m\) to \(n\).

109.

After drawing the line \(y = 2x −1\) and marking the point \(A = (−2, 7)\), Kendall is trying to decide which point on the line is closest to \(A\). The point \(P = (3, 5)\) looks promising. To check that \(P\) really is the point on \(y = 2x − 1\) that is closest to \(A\), what would help Kendall decide? Is \(P\) closest to \(A\)?

110.

Let \(K = (−2, 1)\) and \(M = (3, 4)\). Find coordinates for the two points that divide segment \(KM\) into three congruent segments.

111.

Let \(A = (−5, 2)\) and \(B = (19, 9)\). Find coordinates for the point \(P\) between \(A\) and \(B\) that is three fifths of the way from \(A\) to \(B\). Find coordinates for the point \(Q\) between \(A\) and \(B\) that is three fifths of the way from \(B\) to \(A\).

112.

Given the points \(K = (−2, 1)\) and \(M = (3, 4)\), find coordinates for a point \(J\) that makes \(\angle JKM\) a right angle.

113.

When two lines intersect, four angles are formed. It is believable that the nonadjacent angles in this arrangement are congruent. If you had to prove this to a skeptic, what reasons would you offer? These pairs of angles are called vertical angles.

114.

Find a point on the line \(2x + y = 8\) that is equidistant from the coordinate axes. How many such points are there?

115.

Let \(A = (2, 9)\), \(B = (6, 2)\), and \(C = (10, 10)\). Verify that segments \(AB\) and \(AC\) have the same length. Measure \(\angle ABC\) and \(\angle ACB\). Based on your work, propose a general statement that applies to any triangle that has two sides of equal length. Write an argument supporting your assertion, which might be called the Isosceles Triangle Theorem.

116.

A line goes through the points \((2, 5)\) and \((6, −1)\). Let \(P\) be the point on this line that is closest to the origin. Calculate the coordinates of \(P\).

117.

CHALLENGE: Given that \(P = (−1, −1)\), \(Q = (4, 3)\), \(A = (1, 2)\), and \(B = (7, k)\), find the value of k that makes the line \(AB\) (a) parallel to \(PQ\); (b) perpendicular to \(PQ\).

118.

Let \(A = (−6, −4)\), \(B = (1, −1)\), \(C = (0, −4)\), and \(D = (−7, −7)\). Show that the opposite sides of quadrilateral \(ABCD\) are parallel. Such a quadrilateral is called a parallelogram.

119.

Find the components of a vector that is three fifths as long as \([24, 7]\).

120.

Let \(A = (0, 0)\), \(B = (4, 2)\), and \(C = (1, 3)\), find the exact size of \(\angle CAB\). Justify your answer without your protractor.

121.

Let \(A = (3, 2)\), \(B = (1, 5)\), and \(P = (x, y)\). Find \(x\)- and \(y\)-values that make \(\angle ABP\) a right angle.

122.

(Continuation) Describe the configuration of all such points \(P\).

123.

Find coordinates for the vertices of a lattice rectangle that is three times as long as it is wide with none of the sides horizontal.

124.

Find components for the following vectors \(\overrightarrow {AB}\):

1. \(A = (1, 2)\) and \(B = (3, −7)\)
2. \(A = (2, 3)\) and \(B = (2 + 3t, 3 − 4t)\)

125.

If \(C = (−2, 5)\) and \(D = (−3, 9)\), find components for the vector that points

1. from \(C\) to \(D\)
2. from \(D\) to \(C\)

126.

Show that the lines \(3x − 4y = −8\), \(x = 0\), \(3x − 4y = 12\), and \(x = 4\) form the sides of a rhombus.

127.

Given the points \(E\), \(W\), and \(S\) with the property \(EW= 5\), \(WS = 7\), and \(ES = 12\). What can be said about these three points? What would be true if \(ES\) is less than 12?

128.

Describe a transformation that carries the triangle with vertices \((0, 0)\), \((13, 0)\), and \((3, 2)\) onto the triangle with vertices \((0, 0)\), \((12, 5)\), and \((2, 3)\). Where does your transformation send the point \((6, 0)\)? If you cannot find the exact coordinates, make your best guess.

129.

Suppose that \(\Delta ACT\) has been shown to be congruent to \(\Delta ION\), with vertices \(A\), \(C\), and \(T\) corresponding to vertices \(I\), \(O\), and \(N\), respectively. It is customary to record this result by writing \(\Delta ACT \cong \Delta ION\). Notice that corresponding vertices occupy corresponding positions in the equation. Let \(B = (5, 2)\), \(A = (−1, 3)\), \(G = (−5, −2)\), \(E = (1, −3)\), and \(L = (0, 0)\). Using only these five labels, find as many pairs of congruent triangles as you can, and express the congruences accurately.

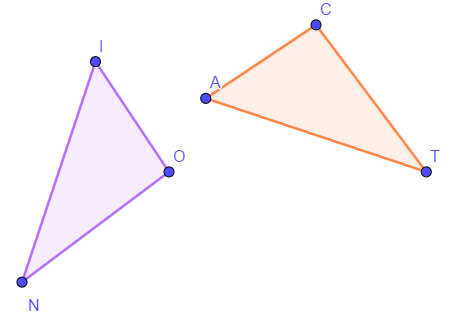
130.

(Continuation) How many ways are there of arranging the six letters of \(\Delta ACT \cong \Delta ION\) to express the two-triangle congruence?

131.

What can be concluded about \(\Delta ABC\) if it is given that

1. \(\Delta ABC \cong \Delta BCA\)?
2. \(\Delta ABC \cong \Delta ACB\)?

132.

Plot points \(K = (−4, −3)\), \(L = (−3, 4)\), \(M = (−6, 3)\), \(X = (0, −5)\), \(Y = (6, −3)\), and \(Z = (5, 0)\). Show that \(\Delta KLM \cong \Delta XZY\). Describe a transformation that transforms \(\Delta KLM\) onto \(\Delta XZY\). Where does this transformation send the point \((−5, 0)\)?

133.

Prove a property of the two acute angles in a right triangle.

134.

Given \(A = (6, 1)\), \(B = (1, 3)\), and \(C = (4, 3)\), find a lattice point \(P\) that makes the segments \({AB}\) and \({CP}\) perpendicular.

135.

(Continuation) Write an equation of a line in point-slope form that describes the set of points \(P\) for which \({AB}\) and \({CP}\) are perpendicular.

136.

Let \(A = (0, 0)\), \(B = (1, 2)\), \(C = (6, 2)\), \(D = (2, −1)\), and \(E = (1, −3)\). Show that \(\angle CAB\) is the same size as \(\angle EAD\). Use GeoGebra to help you solve this problem.

137.

Triangle Inequality Theorem: What must be true about the three sides of a triangle for it to exist?

138.

What is true about all the points that lie on the perpendicular bisector of a segment?

139.

Let \(A = (0, 0)\), \(B = (8, 1)\), \(C = (5, −5)\), \(P = (0, 3)\), \(Q = (7, 7)\), and \(R = (1, 10)\). Prove that \(\angle ABC\) and \(\angle PQR\) have the same size.

140.

(Continuation) Let \(D\) be the point on segment \(AB\) that is exactly 3 units from \(B\), and let \(T\) be the point on segment \(PQ\) that is exactly 3 units from \(Q\). What evidence can you give for the congruence of triangles \(\Delta BCD\) and \(\Delta QRT\)?

141.

The diagonals \(AC\) and \(BD\) of quadrilateral \(ABCD\) intersect at \(O\). Given the information \(AO = BO\) and \(CO = DO\), what can you deduce about the lengths of the sides of the quadrilateral? Prove your response.

142.

An altitude of a triangle is a segment that joins one of the three vertices to a point on the line that contains the opposite side, the intersection being perpendicular. For example, consider the triangle whose vertices are \(A = (0, 0)\), \(B = (8, 0)\), and \(C = (4, 12)\).

1. Find the length of the altitude from \(C\) to side \(AB\).
2. Draw the altitude from \(A\) to \(BC\) and find an equation for the line that contains the altitude from \(A\) to side \(BC\).
3. Find an equation for the line \(BC\).
4. Find coordinates for the point where the altitude from \(A\) meets side \(BC\).
5. Find the length of the altitude from \(A\) to side \(BC\).
6. As a check on your work, calculate \(BC\) and multiply it by your answer to part (e). Compare this result to the result of multiplying \(AB\) by your answer to part (a).
7. Is it possible to deduce the length of the altitude from \(B\) to side \(AC\) from what you have already calculated? Hint: Think about the formula for finding the area of a triangle.

143.

Find a point on the line \(x + 2y = 8\) that is equidistant from the points \((3, 8)\) and \((9, 6)\).

144.

If a quadrilateral is equilateral, its diagonals are perpendicular. True or false? Why?

145.

Make up a geometry problem to go with the equation \(x + 3x + x\sqrt{10} = 42\)

146.

Prove that in a rhombus, the diagonals create four congruent triangles.

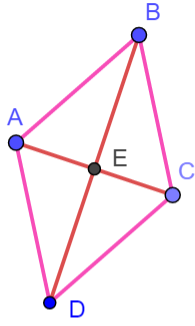
• We know that \(AB \cong BC \cong CD \cong DA\) because _______________________.
• Since \(B\) is equidistant from \(A\) and \(C\), point \(B\) must ________________________________.
• Since \(B\) lies on the perpendicular bisector of \(AC\), __________ is the midpoint of \(AC\), and therefore segment ______ \(\cong\) segment _____.
• Similarly, since \(DC \cong CB\), \(C\) lies on the perpendicular bisector of \(DB\). This means that segment ________ \(\cong\) segment ________.
• So, we can say that \(\Delta AED \cong \Delta AEB \cong \Delta CEB \cong \Delta CED\) by ________________.
• Therefore, four congruent triangles are formed.

147.

Given the following picture, and that \(HF\) and \(JG\) bisect each other at point \(E\), prove \(\angle H \cong \angle F\).

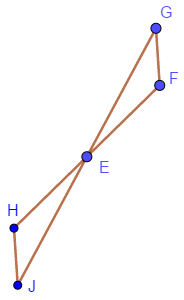
• Since \(HF\) and \(JG\) bisect each other at point \(E\), we can say that ________ \(\cong\) __________ and ________ \(\cong\) _________.
• We can also say that the pair of angles \(\angle \)_______ and \(\angle \)________ are congruent to each other because they are vertical angles.
• Therefore, by _______________ we can say that the triangles __________ and _________ are congruent.
• So, \(\angle H \cong \angle F\) because ________________________.

148.

Let \(A = (−2, 3)\), \(B = (6, 7)\), and \(C = (−1, 6)\).

1. Find an equation for the perpendicular bisector of \(AB\).
2. Find an equation for the perpendicular bisector of \(BC\).
3. Find coordinates for a point \(K\) that is equidistant from \(A\), \(B\), and \(C\).

149.

Consider the triangle defined by \(P = (1, 3)\), \(Q = (2, 5)\), and \(R = (6, 5)\). The transformation defined by \(T(x, y) = (x + 2, y - 1)\) is mathematical notation for translating a point a point two units to the right and one unit down. The point \(P(1, 3)\) becomes \(T(1, 3) = (1 + 2, 3-1) = P'(3, 2)\). Find \(Q'\) and \(R'\). Graph both the original triangle and its image.

150.

(Continuation) The transformation \(T (x, y) = (y + 2, x − 2)\) is a reflection. Verify this by calculating the effect of \(T\) on \(\Delta PQR\). Sketch \(\Delta PQR\), find coordinates for the image points \(P''\), \(Q''\), and \(R''\), and sketch the image \(\Delta P''Q''R''\). Then, identify the mirror line and add it to your sketch. Notice that \(\Delta PQR\) is labeled in a clockwise sense; what about the labels on \(\Delta P''Q''R''\)?