401.

An equilateral \(\Delta ABC\) is inscribed in a circle centered at O. The portion of the circle that lies above chord \(AB\) is called an arc and is written \(\overparen{AB}\). A central angle is an angle whose vertex is at the center of a circle and whose sides are radii. If \(\overparen{AB} = \overparen{BC} = \overparen{AC}\), what is the angular measure of \(\overparen{AB}\)? What is the measure of \(\angle AOB\)? What is the relationship between a central angle and the arc it intercepts?

402.

(Continuation) \(\overparen{AB}\) is called a minor arc and \(\overparen{ACB}\) is called a major arc. Why do you think they are called this? How are \(\overparen{AB}\) and \(\overparen{ACB}\) related?

403.

What is the angular measure of an arc that a diameter intercepts? This arc is called a semicircle.

404.

If the ratio of the areas of two triangles is \(18:8\), what is the ratio of similarity?

405.

The vertices of a square with sides parallel to the coordinate axes lie on the circle of radius 5 whose center is at the origin. Find coordinates for the four vertices of this square.

406.

Draw a circle and label one of its diameters \(AB\). Choose any other point on the circle and call it \(C\). What can you say about the size of \(\angle ACB\)? Does it depend on which \(C\) you chose? Justify your response.

407.

A square pyramid is a pyramid with a square base and four triangular lateral faces. The slant height is the distance from the vertex of the pyramid along a lateral face to the midpoint of a base edge. If the slant height is 10 cm and an edge of the square is 12 cm, what is the altitude of this pyramid?

408.

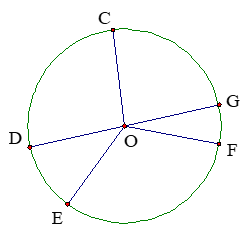
Circle \(O\) has diameter \(DG\) and central angles \(\angle COG = 86°\), \(\angle DOE = 25°\), and \(\angle FOG = 15°\). Find the angular size of minor arcs \(\overparen{CG}\), \(\overparen{CF}\), \(\overparen{EF}\) and major arc \(\overparen{DGF}\) ̂.

409.

A regular pentagon can be dissected into 5 isosceles triangles whose vertex angle is at the center of the pentagon. The height of the triangles is 10 cm. Find the area of this pentagon.

410.

The area of a circle: A regular hundred-sided polygon with side length of very close to \(b=2\) is inscribed in a circle with radius of 32 (do not attempt to draw this polygon!)

1. Show that the perimeter of the polygon is approximately equal to the circumference of the circle.
2. Show that the height of a central triangle of the polygon is approximately equal to the radius of the circle.
3. You can write the area of the polygon as \(A_{polygon}=100\cdot \) area of a central triangle. Justify rewriting this expression as \(A_{polygon}=100\cdot b\cdot \frac{1}{2}\cdot h\).
4. Now substitute \(2πr\) for \(100\cdot b\). Why can you do this? Please simplify your expression.
5. Then substitute \(r\) for \(h\). Why can you do this?
6. Simplify your expression for the area of the circle.

411.

If two chords in the same circle have the same length, then their minor arcs have the same length, too. True or false? Explain. What about the converse statement? Is it true? Why?

412.

The circle \(x^2 + y^2 = 25\) goes through \(A = (5, 0)\) and \(B = (3, 4)\). To the nearest tenth of a degree, find the angular size of the minor arc \(\overparen{AB}\). Let point \(O\) be \((0, 0)\), now find the measure of \(\angle OBA\).

413.

The sides of a triangle are found to be 10 cm, 14 cm, and 16 cm long, while the sides of another triangle are found to be 15 cm, 21 cm, and 24 cm long. Based on this information, what can you say about the angles of these triangles?

414.

In mathematical discussion, a right prism is defined to be a solid figure that has two parallel, congruent polygonal bases, and rectangular lateral faces. How would you find the volume of such a figure? Explain your method.

415.

In \(\Delta ABC\), it is given that \(\angle BCA\) is right. Let \(a = BC\), \(b = CA\), and \(c = AB\). Using \(a\), \(b\), and \(c\), express the sine, cosine, and tangent ratios of acute angles \(\angle A\) and \(\angle B\).

416.

The sine of a 38° angle is some number \(r\). Without using your calculator, find the angle size whose cosine is the same number \(r\).

417.

On a circle whose center is \(O\), using your protractor or GeoGebra, mark points \(P\) and \(A\) so that minor arc \(\overparen {PA}\) is a 46° arc. GeoGebra has a tool called "Angle with Given Size" near the angle measurement tool to help you draw the correct angle. What does this tell you about \(\angle POA\)? Extend \(PO\) to meet the circle again at \(T\). What is the size of \(\angle PTA\)? This angle is inscribed in the circle, because its vertex is on the circle. The arc \(\overparen {PA}\) is intercepted by \(\angle PTA\). Make a conjecture about arcs intercepted by inscribed angles.

418.

(Continuation) Confirm your conjecture about inscribed angles and the arcs they intercept using GeoGebra. To measure the arc, select one endpoint, then the center of the circle, then the final endpoint.

419.

Given side lengths of an isosceles triangle, describe the process you would use to calculate the sizes of its angles.

420.

If \(P\) and \(Q\) are points on a circle, then the center of the circle must be on the perpendicular bisector of chord \(PQ\). Explain. Which point on the chord is closest to the center? Why?

421.

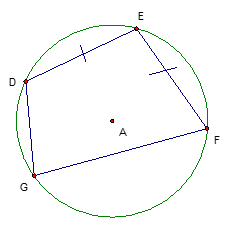
The diagram below shows quadrilateral \(DEFG\) in inscribed in circle \(A\). \(ED \cong EF\), \(\angle E=100°\) and \(\angle F=70°\). Find the measures of the four minor arcs.

422.

Given that \(\Delta ABC \sim \Delta PQR\), write the three-term proportion that describes how the six sides of these figures are related.

423.

A circle of radius 5 is circumscribed about a regular hexagon. Find the area of the hexagon.

424.

A regular hexagon has an inscribed circle of radius 4. Find the area of the hexagon.

425.

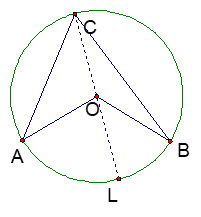
CHALLENGE: The Star Trek Theorem: You have found that an inscribed angle is half the measure of the arc that it intercepts.

1. Given a circle centered at \(O\), let \(A\), \(B\) and \(C\) be points on the circle such that \(\overparen{AB} \ne \overparen{BC}\) and \(CL\) is a diameter. Why must \(\Delta AOC\) and \(\Delta BOC\) be isosceles?
2. State the pairs of angles that must be congruent in these isosceles triangles.
3. Using the Exterior Angle Theorem, find expressions for the measures of \(\angle AOL\) and \(\angle BOL\).
4. Based on your statement in part c, explain the statements \(\angle ACO = {\textstyle{1 \over 2}}\angle AOL\) and \(\angle OCB = {\textstyle{1 \over 2}}\angle BOL\).
5. Now find an expression for \(\angle ACB\) and simplify to prove that it equals \({\textstyle{1 \over 2}}\angle AOB\).

426.

Draw a circle in GeoGebra or one on paper with at least a 2-inch radius. Mark four points randomly (not evenly spaced) on the circle. Label them consecutively \(G\), \(E\), \(O\), and \(M\). Measure \(\angle GEO\) and \(\angle GMO\). Could you have predicted the result? Name another pair of angles that would have produced the same result.

427.

A circular park 80 meters in diameter has a straight path non-diameter chord cutting across it. It is 24 meters from the center of the park to the closest point on this path. How long is the path?

428.

\(\Delta ABC\) is inscribed in a circle. Given that \(\overparen{AB}\) is a 40° arc and \(\angle ABC\) is a 50° angle, find the sizes of the other arcs and angles in the figure.

429.

Algebraically, find the intersections of the line \(y = 2x – 5\) with the circle \(x^2 + y^2 = 25\). Then use your calculator or GeoGebra to find the intersections of the line \(−2x + 11y = 25\) with the same circle. Show that these lines create chords of equal length when they intersect the circle. With your protractor, measure the inscribed angle formed by these chords.

430.

(Continuation) Calculate the angle between the chords to the nearest tenth of a degree. What is the angular size of the arc that is intercepted by this inscribed angle?

431.

A triangle has a 3-inch side, a 4-inch side, and a 5-inch side. The altitude drawn to the 5-inch side cuts this side into segments of what lengths?

432.

A chord 6 cm long is 2 cm from the center of a circle. How long is a chord that is 1 cm from the center of the same circle?

433.

By using the triangle whose sides have lengths \(1\), \(\sqrt{3}\) and \(2\), you should be able to write expressions for the sine, cosine, and tangent of a 30° angle without using a calculator. Do so. Write your answers in simplest radical form. Use a calculator to check your answers.

434.

Find all the angles in a 5-12-13 triangle.

435.

A trapezoid has two 65° angles and 8-inch and 12-inch parallel sides. How long are the non-parallel sides? What is the area enclosed by this figure?

436.

Find the area of a regular 36-sided polygon inscribed in a circle of radius 20 cm. If this polygon were the base of a right prism with an altitude of 50 cm, what would the volume of the prism be?

437.

You are at the scenic overlook at Thacher Park looking through the panoramic viewer that is looking straight ahead. How many degrees must you tilt the viewer directly downward from the horizontal to see the Egg in Albany, which you know to be 30 miles away. The scenic overlook is two-tenths of a mile high.

438.

Draw trapezoid \(ABCD\) so that \(AB\) is parallel to \(CD\). Draw in the diagonals of the trapezoid. Label the intersection as \(E\). Show that \(\Delta ABE \sim \Delta CDE\) i.e. that the triangles are similar.

439.

The area of an equilateral triangle is \(100\sqrt{3}\) square inches. How long are its sides?

440.

The points \(A = (0, 13)\) and \(B = (12, 5)\) lie on a circle whose center is at the origin. Show that the perpendicular bisector of \(AB\) goes through the origin.

441.

The areas of two similar triangles are 24 cm² and 54 cm². The smaller triangle has a 6-cm side. How long is the corresponding side of the larger triangle?

442.

Given that \(\theta\) (Greek “theta”) stands for the degree size of an acute angle, fill in the blank space between the parentheses to create a true statement: \(\sin {\theta} = \cos (\;\;\;\;\;)\).

443.

If the ratio of similarity between two triangles is \(3:5\), what is the ratio of the areas of these triangles?

444.

How much evidence is needed to be sure that two triangles are similar?

445.

Trapezoid \(ABCD\) has parallel sides \(AB\) and \(CD\), of lengths 8 and 24, respectively. Diagonals \(AC\) and \(BD\) intersect at \(E\), and the length of \(AC = 15\). Find the lengths of \(AE\) and \(EC\).

446.

CHALLENGE: Let \(A = (0, 0)\), \(B = (4, 0)\), and \(C = (4, 3)\). Mark point \(D\) so that \(\angle ACD\) is a right angle and \(\angle DAC\) is a 45° angle. Find coordinates for \(D\). Find the tangent of \(\angle DAB\).

447.

A regular octagon has a perimeter of 64 cm. Find its area.

448.

\(\Delta ABC\) has \(P\) on \(AC\), \(Q\) on \(AB\), and \(\angle APQ\) equal to \(\angle B\). The lengths \(AP = 3\), \(AQ = 4\), and \(PC = 5\) are given. Find the length of \(AB\).

449.

A cyclic quadrilateral is a quadrilateral whose vertices are points on a circle. Draw a cyclic quadrilateral \(SPAM\) in which the size of \(\angle SPA\) is 110°. What is the size of \(\angle AMS\)? Would your answer change if \(M\) were replaced by a different point on major arc \(\overparen {SA}\)?

450.

If \(A = (3, 1)\), \(B = (3, 4)\), and \(C = (8, 1)\) find the measure of \(\angle B\).