451.

A 20-inch chord is drawn in a circle with a 12-inch radius. What is the angular size of the minor arc of the chord? What is the length of the arc, to the nearest tenth of an inch?

452.

When you walk into Weaver Hall there are two large regular octagonal pillars. The edges are 6.5 in. and they are 9 feet tall. How much granite was needed to build these pillars?

453.

Quadrilateral \(WISH\) is cyclic. Diagonals \(WS\) and \(HI\) intersect at \(K\). Given that arc \(WI\) is 100° and arc \(SH\) is 80°, find the sizes of as many angles in the figure as you can. Note: \(K\) is not the center of the circle.

454.

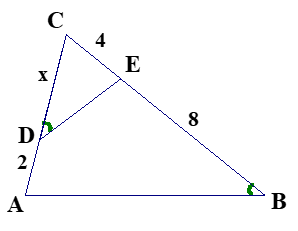
Refer to the figure, in which angles \(\angle ABE\) and \(\angle CDE\) are equal in size and various segments have been marked with their lengths. Find \(x\).

455.

Draw the line \(y = 2x − 5\) and the circle \(x^2 + y^2 = 5\). Use algebra to show that these graphs touch at only one point. It is customary to say that a line and a circle are tangent if they have exactly one point in common.

456.

(Continuation) Find the slope of the segment that joins the point of tangency to the center of the circle and compare your answer with the slope of the line \(y = 2x − 5\). What do you notice?

457.

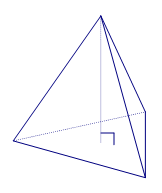
Given that \(ABCDEFGH\) is a cube (shown below), what is the relationship between the cube and the three square pyramids \(ADHEG\), \(ABCDG\), and \(ABFEG\)?

458.

Draw a chord \(AB\) that is 16 cm long in a circle whose radius is 12 cm. Calculate the angular size of minor arc \(\overparen {AB}\).

459.

Show that the line \(y = 10 − 3x\) is tangent to the circle \(x^2 + y^2 = 10\). Find an equation for the line perpendicular to the tangent line at the point of tangency. Show that this line goes through the center of the circle.

460.

Let \(A = (4, 6)\), \(B = (6, 0)\), and \(C = (9, 9)\). Find the size of \(\angle BAC\).

461.

Segment \(AB\), which is 25 inches long, is the diameter of a circle. Chord \(PQ\) meets \(AB\) perpendicularly at \(C\), where \(AC = 16\) in. Find the length of \(PQ\).

462.

Prove that the arcs between any two parallel chords in a circle must be the same size.

463.

Two Tangent Theorem. From any point \(P\) outside a given circle, there are two lines through \(P\) that are tangent to the circle. Explain why the distance from \(P\) to one of the points of tangency is the same as the distance from \(P\) to the other point of tangency. What special quadrilateral is formed by the center of the circle, the points of tangency, and \(P\)?

464.

The altitude of a regular triangular pyramid is the segment connecting a vertex to the centroid of the opposite face. A regular triangular pyramid has edges of length 6 in. How tall is such a pyramid, to the nearest hundredth of an inch?

465.

A 72° arc \(\overparen {AB}\) is drawn in a circle of radius 8 cm. How long is chord \(AB\)?

466.

Find the perimeter of a regular 360-sided polygon that is inscribed in a circle of radius 5 inches. If someone did not remember the formula for the circumference of a circle, how could that person use a calculator’s trigonometric functions to find the circumference of a circle with a 5-inch radius?

467.

The segments \(GA\) and \(GB\) are tangent at points \(A\) and \(B\) to a circle with center \(O\). \(\angle AGB\) is a 60° angle. Given that \(GA = 12 \sqrt{3}\) cm, find the distance \(GO\). Find the distance from \(G\) to the nearest point on the circle.

468.

A circle \(T\) has two tangents that intersect at 54° at point \(M\). The points of tangency are \(A\) and \(H\). What is the angular size of \(\overparen {AH}\)̂?

469.

The Great Pyramid at Giza was originally 483 feet tall, and it had a square base that was 756 feet on a side. It was built from rectangular stone blocks measuring 7 feet by 7 feet by 15 feet. Such a block weighs seventy tons. Approximately how many tons of stone were used to build the Great Pyramid? The volume of a pyramid is one third the base area times the height.

470.

What is the difference between the measure of an arc and the length of an arc?

471.

A group of 12 students is making a pizza so that each student will get one slice. Since only 4 of them like olives, they will put olives only on 4 slices. If they are sharing a 16-in.-diameter pizza, what is the area of the part the pizza covered with olives?

Spreadsheet Lab #6: Areas of Regular Polygons

472.

A triangle that has a 50° angle and a 60° angle is inscribed in a circle of radius 25 inches. The circle is divided into three arcs by the vertices of the triangle. To the nearest tenth of an inch, find the lengths of these three arcs.

473.

Stacy wants to decorate the side of a cylindrical can by using a rectangular piece of paper and wrapping it around the can. The paper is 21.3 cm by 27.5 cm. Find the two possible diameters of the cans that Stacy could use. (Assume the paper fits exactly).

474.

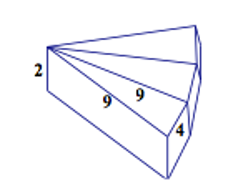
A wedge of cheese is 2 inches tall. The triangular base of this right prism has two 9-inch edges and a 4-inch edge. Several congruent wedges are arranged around a common 2-inch segment, as shown. How many wedges does it take to complete this wheel? What is the volume of the wheel, to the nearest cubic inch?

475.

The segments \(GA\) and \(GB\) are tangent to a circle at \(A\) and \(B\), and \(\angle AGB\) is a 48° angle. Given that \(GA\) = 12 cm, find the distance from \(G\) to the nearest point on the circle.

476.

A 16.0-inch chord is drawn in a circle whose radius is 10.0 inches. What is the angular size of the minor arc of this chord? What is the length of the arc, to the nearest tenth of an inch?

477.

The line \(x + 2y = 5\) divides the circle \(x^2 + y^2 = 25\) into two arcs. Find the lengths of the arcs.

478.

(Continuation) A sector is a region formed by two radii and an arc of a circle. Find the area of the smaller sector.

479.

The equation of a circle is \(x^2+y^2=50\), find the area of the circle.

480.

If the area of a circle centered at the origin is \(40\pi\), write the equation for this circle.

481.

Write the equation of the circle that passes through the vertices of the triangle defined by \((−1, −7)\), \((5, 5)\), and \((7, 1)\).

482.

Alex’s dog, Fluffy, is tied with a 20 ft rope to the center of the bottom of the back wall of the shed, which has dimensions of 14 ft by 18 ft. If the back wall is the longer wall, over what area can Fluffy play, to the nearest square foot? Would your answer change if the back wall was 14 ft instead?

483.

All triangles have circumscribed circles. Why? What property must a given quadrilateral hold in order to have a circumscribed circle? Explain.

484.

Pyramid \(TABCD\) has a square base \(ABCD\) with 20-cm base edges. The lateral edges that meet at \(T\) are 27 cm long. Make a diagram of \(TABCD\), showing \(F\), the point of \(ABCD\) closest to \(T\). To the nearest 0.1 cm, find the height \(TF\). Find the volume of \(TABCD\), to the nearest cm³.

485.

(Continuation) Find the slant height of pyramid \(TABCD\). The slant height is the height of the lateral face.

486.

Two of the tangents to a circle meet at \(Q\), which is 25 cm from the center. The circle has a 7-cm radius. To the nearest tenth of a degree, find the angle formed at \(Q\) by the tangents.

487.

CHALLENGE: Which is the better (tighter) fit: A round peg in a square hole or a square peg in a round hole?

488.

From the top of Mt Washington, which is 6,288 feet above sea level, how far is it to the horizon? Assume that the Earth has a 3,962-mile radius and give your answer to the nearest mile.

489.

What is the minimum amount of wrapping paper needed to wrap a box with dimensions 20 cm by 10 cm by 30 cm?

490.

Which polygons can have circumscribed circles? Explain.

491.

A paper towel tube has a diameter of 1.7 inches and a height of 11 inches. If the tube were cut and unfolded to form a rectangle, what would be the area of the rectangle?

492.

Find the area of a kite whose longer diagonal is divided into two parts that are 4 and 12 and whose shorter side is 5.

493.

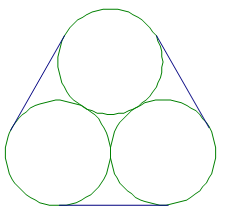
CHALLENGE: The figure shows three circular pipes, all with 12-inch diameters, that are strapped together by a metal band. How long is the band?

494.

CHALLENGE: (Continuation) Suppose that four pipes are strapped together with a snugly-fitting metal band. How long is the band?

495.

The lateral edges of a regular hexagonal pyramid are all 20 cm long, and the base edges are all 16 cm long. To the nearest cm³, what is the volume of this pyramid? To the nearest square cm, what is the combined area of the base and six lateral faces?

496.

Find the total grazing area of the goat G represented in the figure (a top view) shown at right. The animal is tied to a corner of a 40’ × 40’ barn, by an 80’ rope. One of the sides of the barn is extended by a fence. Assume that there is grass everywhere except inside the barn.

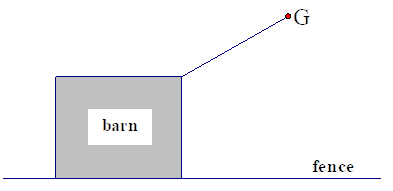
497.

Surface area of a Sphere: The surface area of a sphere is found using the formula \(4πr^2\). Find the surface area of the Earth, given that its diameter is 7924 miles.

498.

For any pyramid, the volume is \(V = {\textstyle{1 \over 3}}base\_area \cdot height\). A cone is a pyramid with a circular base. Find the volume of a cone with a slant height of 13 in. and a diameter of 10 in. Use correct units in your answer.

499.

A sector of a circle is enclosed by two 12.0-inch radii and a 9.0-inch arc. The sector’s perimeter is therefore 33.0 inches. What is the area of this sector, to the nearest tenth of a square inch? What is the central angle of the sector, to the nearest tenth of a degree?

500.

CHALLENGE: (Continuation) There is another circular sector – part of a circle of a different size – that has the same 33-inch perimeter and that encloses the same area. Find its central angle, radius, and arc length, rounding the lengths to the nearest tenth of an inch.

501.

The radius of the Sun is 109 times the radius of the Earth. Find the surface area of the Sun.

502.

The radius of a circular sector is \(r\). The central angle of the sector is \(\theta\). Write formulas for the arc length and the perimeter of the sector.

503.

Schuyler has made some glass prisms to be sold as window decorations. Each prism is four inches tall and has a regular hexagonal base with half-inch sides. They are to be shipped in cylindrical tubes that are 4 inches tall. What radius should Schuyler use for the tubes? Once a prism is inserted into its tube, what volume remains for packing material?

504.

CHALLENGE: Suppose that chords \(AB\) and \(BC\) have the same lengths as chords \(PQ\) and \(QR\), respectively, with all six points belonging to the same circle (they are concyclic). Is this enough information to conclude that chords \(AC\) and \(PR\) have the same length? Explain.

505.

A conical cup has a 10-cm diameter and is 12 cm deep. How much can this cup hold?

506.

(Continuation) Water in the cup is 6 cm deep. What percentage of the cup is filled?

507.

Imagine the interior of a sphere can be approximated by numerous cones, each with a base area, \(B\), height of \(r\), and vertex at the center of the sphere. What formula do you already know that describes the sum of the base areas?

508.

(Continuation) Given this approximation of a sphere, develop a formula for its volume.

509.

A sphere of ice cream is placed on an ice cream cone. Both have a diameter of 8 cm. The height of the cone is 12 cm. Will all the ice cream, if pushed down into the cone, fit?

510.

The base radius of a cone is 6 inches, and the cone is 8 inches tall. To the nearest square inch, what is the area of the lateral surface of the cone? What is the total surface area of the cone?

511.

CHALLENGE: If the surface area of a sphere equals the surface area of a cube, what is the ratio of the volume of the sphere to the volume of the cube?

512.

Three tennis balls fit snugly inside a cylindrical can. What percent of the available space inside the can is occupied by the balls?

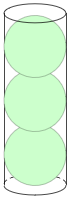
513.

The areas of two circles are in the ratio of \(50:32\). If the radius of the larger circle is 10, what is the radius of the smaller circle?

514.

CHALLENGE: To make their product seem like a better bargain, the Chock-a-Lot Candy Company increased the size of their chocolate balls, from a 2-cm diameter to a 3-cm diameter, without increasing the price. In fact, the new balls still contain the same amount of chocolate, because they are hollow spherical shells, while the 2-cm balls are solid chocolate. How thick are the spherical chocolate shells that Chock-a-Lot is now selling?

515.

The area of a sector of a circle with radius 12 is 16π cm². What is the central angle of this sector?

516.

Find the perimeter of the semicircle with radius 10.