351.

Compare the quadrilateral whose vertices are \(A=(0, 0)\), \(B = (6, 2)\), \(C = (5, 5)\), \(D = (−1, 3)\) with the quadrilateral whose vertices are \(P = (9, 0)\), \(Q = (9, 2)\), \(R = (8, 2)\), and \(S = (8, 0)\). Show that these two figures are similar. Is there a dilation that takes \(ABCD\) to \(PQRS\)?

352.

Write an equation using the distance formula that says that \(P = (x, y)\) is 5 units from \((0, 0)\). Plot several such points. What is the configuration of all such points called? How many are lattice points?

353.

(Continuation) Explain how you could use the Pythagorean Theorem to obtain the same result.

354.

Does a dilation transform any figure into a similar figure? If you know that two triangles are similar does that mean that they are dilations of one another?

355.

What is the length of a side of an equilateral triangle whose altitude is 16?

356.

When you take the sine of 30° using your calculator you get 0.5. What do you think SIN-1(0.5) (or ASIN(0.5)) is? Use your calculator to test your conjecture. Find SIN-1(0.3) and SIN-1⁡(3/5). What do these values represent?

357.

When \(\Delta ABC\) is similar to \(\Delta PQR\), with \(A\), \(B\), and \(C\) corresponding to \(P\), \(Q\), and \(R\), respectively, it is customary to write \(\Delta ABC \sim \Delta PQR\). Suppose that \(AB = 4\), \(BC = 5\), \(CA = 6\), and \(RP = 9\). Find \(PQ\) and \(QR\).

358.

To the nearest tenth of a degree, find the sizes of the acute angles in the right triangle whose hypotenuse is 2.5 times as long as its short leg.

359.

CHALLENGE: A triangle has a 60° angle and a 45° angle and the side opposite the 45° angle is 240 mm long. To the nearest mm, how long is the side opposite the 60° angle?

360.

One triangle has sides that are 5 cm, 7 cm, and 8 cm long; the longest side of a similar triangle is 6 cm long. How long are the other two sides?

361.

Judy is driving along a highway that is climbing a steady 9° slope. After driving for two kilometers along this road, how much altitude has Judy gained?

362.

(Continuation) How far must Judy travel in order to gain a kilometer of altitude?

363.

If an altitude is also the side of a triangle, what do you know about the triangle?

364.

If two polygons are similar, explain why the corresponding angles are the same size. What is the converse of this statement? Is it true?

365.

AA Similarity Postulate: If two corresponding angles of a triangle are equal in size to the angles of another triangle, then the triangles are similar. Justify this statement. State the converse of this statement. Is it true?

366.

Is it possible to draw a triangle with the given sides? If it is possible, state whether it is acute, right, or obtuse. If it is not possible, say no and sketch why.

1. \(9, 6, 5\)
2. \(3\sqrt {3}, 9, 6\sqrt 3\)
3. \(8.6, 2.4, 6.2\)

367.

The area of an equilateral triangle with \(m\)-inch sides is 8 square inches. What is the area of a regular hexagon that has \(m\)-inch sides?

368.

A parallelogram has 10-inch and 18-inch sides and an area of 144 in².

1. How far apart are the 18-inch sides?
2. How far apart are the 10-inch sides?
3. What are the angles of the parallelogram?
4. How long are the diagonals?

369.

Write an equation that describes all the points on the circle whose center is at the origin and whose radius is

1. 13
2. 6
3. \(r\)

370.

If the lengths of the midsegments of a triangle are 3, 4, and 5, what is the perimeter of the triangle?

371.

During the time that they were moving the kitchen, the dining hall packed our old round plates in square boxes with a perimeter of 36 inches. If the plates fit snugly in one stack in the box, one plate per layer, what is the circumference of each plate?

372.

(Continuation) Each dining hall saucer has a circumference of 12.57 in. Can four saucers fit on a single layer in the same square box? Justify your answer.

373.

Graph the circle whose equation is \({x^2} + {y^2} = 64\). What is its radius? What do the equations \({x^2} + {y^2} = 1\), \({x^2} + {y^2} = 40\), and \({x^2} + {y^2} = k\) all have in common? How do they differ?

374.

Let \(A = (0, 5)\), \(B = (−2, 1)\), \(C = (6, −1)\), and \(P = (12, 9)\). Let \(A'\), \(B'\), and \(C'\) be the midpoints of segments \(PA\), \(PB\), and \(PC\), respectively. After you make a diagram, identify the center and the scale factor of the dilation that transforms \(\Delta ABC\) onto \(\Delta A'B'C'\).

375.

375. Taylor let out 120 meters of kite string and wondered how high the kite has risen. Taylor used a phone app to measure the angle of elevation of the kite string and found it to be 63°. How high is the kite to the nearest meter? What (unrealistic) assumptions did you make in answering this question?

376.

Without using a calculator, find the sine of a 45° angle. Use a calculator to check your answer.

377.

Using GeoGebra: Let \(A = (1, 5)\), \(B = (3, 1)\), \(C = (5, 4)\), \(A' = (5, 9)\), \(B' = (11, −3)\), and \(C' = (17, 6)\). Show that there is a dilation that transforms \(\Delta ABC\) onto \(\Delta A'B'C'\). In other words, find the dilation center and the scale factor.

378.

(Continuation) Calculate the areas of triangles \(\Delta ABC\) and \(\Delta A'B'C'\). Are your answers related in a predictable way?

379.

If the central angle of a slice of pizza is 36°, how many pieces are in the pizza?

380.

(Continuation) A 12-inch-diameter pizza is evenly divided into 8 pieces. What is the length of the crust of one piece?

381.

The vertices of \(\Delta ABC\) are \(A = (−5, −12)\), \(B = (5, −12)\), and \(C = (5, 12)\). Confirm that the circumcenter of \(\Delta ABC\) lies at the origin. What is the equation for the circumscribed circle?

382.

If the sides of a triangle are 13, 14, and 15 cm long, then the altitude drawn to the 14-cm side is 12 cm long. How long are the other two altitudes? Which side has the longest altitude?

383.

(Continuation) How long are the altitudes of the triangle if you double the lengths of its sides?

384.

Let \(A = (6, 0)\), \(B = (0, 8)\), \(C = (0, 0)\). In \(\Delta ABC\), let \(F\) be the point of intersection of the altitude drawn from \(C\) to side \(AB\).

1. Explain why the angles of triangles \(\Delta ABC\), \(\Delta CBF\), and \(\Delta ACF\) are the same.
2. Find coordinates for \(F\) and use them to calculate the exact lengths \(FA\), \(FB\), and \(FC\).
3. Compare the sides of \(\Delta ABC\) with the sides of \(\Delta ACF\). What do you notice?

385.

What happens to the area of a triangle if its dimensions are doubled?

386.

CHALLENGE: A rectangular sheet of paper is 20.5 cm wide. When it is folded in half, with the crease running parallel to the 20.5-cm sides, the resulting rectangle is the same shape as the unfolded sheet. Find the length of the sheet, to the nearest tenth of a cm. (In Europe, the shape of notebook paper is determined by this similarity property).

387.

SAS Similarity,. Use your protractor to carefully draw a triangle that has a 3-cm side, a 4-cm side, and whose included angle is 40°. Construct a second triangle that has a 7.5-cm side, a 10-cm side, and whose included angle is also 40°. Measure the remaining parts of these triangles. Could you have anticipated the results? Explain.

388.

A regular polygon is inscribed in a circle. What happens to the regular polygon as the number of sides increases?

389.

Sketch the circle whose equation is \(x^2 + y^2 = 100\). Using the same system of coordinate axes, graph the line \(x + 3y = 10\), which should intersect the circle twice: at \(A = (10, 0)\) and at another point \(B\) in the second quadrant. Estimate the coordinates of \(B\). Now use algebra to find them exactly. Segment \(AB\) is called a chord of the circle.

390.

(Continuation) Find coordinates for a point \(C\) on the circle that makes chords \(AB\) and \(AC\) have equal length.

391.

What is the radius of the smallest circle that surrounds a 5-by-12 rectangle?

392.

Baking Powder is made up of Baking Soda, Cream of Tartar and sometimes Corn Starch in a ratio of \(1:2:1\). If you need 2 Tablespoons of Baking Powder, how much of each ingredient do you need?

393.

CHALLENGE: Without doing any calculation, what can you say about the tangent of a \(k\)-degree angle, when \(k\) is a number between 90 and 180? Explain your response, then check with your calculator.

394.

Ask your calculator for the sine of a 56° angle, then for the cosine of a 34° angle. Ask your calculator for the sine of a 23° angle, then for the cosine of a 67° angle. The word cosine is an abbreviation of sine of the complement. Explain the terminology.

395.

(Continuation) How can you represent the cosine of an angle in terms of a ratio?

396.

A right triangle has a 123-foot hypotenuse and a 38-foot leg. To the nearest tenth of a degree, what are the sizes of its acute angles?

397.

The line \(y = x + 2\) intersects the circle \(x^2 + y^2 = 10\) in two points. Call the third quadrant point \(R\) and the first-quadrant point \(E\) and find their coordinates. Let \(D\) be the point where the line through \(R\) and the center of the circle intersects the circle again. The chord \(DR\) is an example of a diameter. Show that \(\Delta RED\) is a right triangle.

398.

To the nearest tenth of a degree, find the angles of the triangle with vertices \((0, 0)\), \((6, 3)\), and \((1, 8)\). Use your protractor to check your calculations and explain your method.

399.

Playing cards measure 2.25 inches by 3.5 inches. A full deck of fifty-two cards is 0.75 inches high. What is the volume of a deck of cards? If the cards were uniformly shifted (turning the bottom illustration into the top illustration), would this volume be affected?

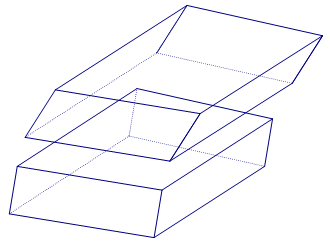
400.

In a right triangle, the 58-cm hypotenuse makes a 51° angle with one of the legs. To the nearest tenth of a cm, how long is that leg? Once you have the answer, find some other ways to calculate the length of the other leg. They should all give the same answer, of course.