302.

Standing 50 meters from the base of a fir tree, Rory measured an angle of elevation of 33° to the top of the tree with a protractor. The angle of elevation is the angle formed by the horizontal and the line of sight ray. How tall is the tree?

303.

Given regular hexagon \(BAGELS\), show that \(\Delta SEA\) is an equilateral triangle.

304.

When the sun has risen 32° above the horizon, Natalia casts a shadow that is 9 feet 2 inches long. How tall is Natalia to the nearest inch?

305.

Standing on a cliff 380 meters above the sea, Mar sees an approaching ship and measures its angle of depression, obtaining 9°. How far from shore is the ship?

306.

(Continuation) Now Mar sights a second ship beyond the first. The angle of depression of the second ship is 5°. How far apart are the ships?

307.

What is the radius of the smallest circle that encloses an equilateral triangle with 12-inch sides? What is the radius of the largest circle that will fit inside the same triangle?

308.

Let \(A = (0, 0)\), \(B = (4, 0)\), and \(C = (4, 3)\). Measure \(\angle CAB\) with your protractor. What is the slope of \(AC\)? Use your calculator to compare the tangent of the angle you measured with the slope. By trial-and-error, find an angle that is a better approximation of the measure of \(\angle CAB\).

309.

(Continuation) On a TI-84 calculator, enter the expression TAN-1(0.75). On a NumWorks calculator, enter ATAN(0.75) Compare this answer with the approximation you obtained for the measure of \(\angle CAB\). What does the TAN-1 or ATAN button do? (TAN-1 is said as “inverse tangent” and ATAN is said as “arctangent.”)

310.

A five-foot Emma student casts an eight-foot shadow. How high is the sun in the sky? This is another way of asking for the angle of elevation of the sun.

311.

An isosceles trapezoid has sides of lengths 9, 10, 21, and 10. Find the distance that separates the parallel sides then find the length of the diagonals. Finally, find the angles of the trapezoid, to the nearest tenth of a degree.

312.

One day at the beach, Kelly flies a kite, whose string makes a 37° elevation angle with the ground. Kelly is 130 feet from the point directly below the kite. How high above the ground is the kite, to the nearest foot?

313.

Hexagon \(ABCDEF\) is regular. Prove that segments \(AE\) and \(ED\) are perpendicular.

314.

What angle does the line \(y = {\textstyle{2 \over 5}}x\) make with the x-axis?

315.

Suppose that \(PQRS\) is a rhombus, with \(PQ = 12\) and a 60° angle at \(Q\). How long are the diagonals \(PR\) and \(QS\)?

316.

Given a rectangular card that is 5 inches long and 3 inches wide, what does it mean for another rectangular card to have the same shape? Describe a couple of examples.

317.

CHALLENGE: The Varignon quadrilateral. A quadrilateral has diagonals of lengths 8 and 10. The midpoints of the sides of this figure are joined to form a new quadrilateral. What is the perimeter of the new quadrilateral? What is special about it?

318.

The hypotenuse of a right triangle is twice as long as one of the legs. How long is the other leg? What is the size of the smallest angle?

319.

What are the angle sizes in a trapezoid whose sides have lengths 6, 20, 6, and 26?

320.

Atiba wants to measure the width of the Hudson River. Standing under a tree \(T\) on the riverbank, Atiba sights a rock at the nearest point \(R\) on the opposite bank. Then Atiba walks to a point \(P\) on the riverbank that is 50.0 meters from \(T\), and makes \(\angle RTP\) a right angle. Atiba then measures \(\angle RPT\) and obtains 76.8°. How wide is the river?

321.

The legs of an isosceles right triangle have a length of \(s\). What is the length of the hypotenuse with respect to \(s\)?

322.

A regular \(n\)-sided polygon has exterior angles of \(m\) degrees each. Express \(m\) in terms of \(n\).

323.

How tall is an isosceles triangle, if its base is 30 cm long and both of its base angles are 72°?

324.

A triangle has sides in the ratio \(1:2:\sqrt 3 \). Draw a triangle with this scale. What can you say about this triangle?

325.

In an Emma Willard Freshman class there are 74 students, and the \(day : boarder\) ratio is approximately \(3:5\).

1. How many students in that class are boarders?
2. How many day students would you expect to find in a freshman seminar class of fifteen students?

Explain.

326.

Find the equation of a line passing through the origin that makes an angle of 52° with the x-axis.

327.

Special Right Triangles. There are special right triangles with integer valued sides. These are called Pythagorean Triples. There are two other special right triangles commonly used in mathematics that do not have integer valued sides. One of these is a 45°-45°-90° triangle. What is the other one?

328.

In the figure below, the shaded triangle has area 15. Find the area of the unshaded triangle.

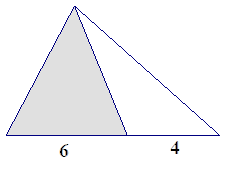
329.

To the nearest tenth of a degree, how large are the congruent angles of an isosceles triangle that is exactly as tall as it is wide? (There is more than one interpretation).

330.

Rectangle \(ABCD\) has \(AB = 16\) and \(BC = 6\). Let \(M\) be the midpoint of side \(AD\) and \(N\) be the midpoint of side \(CD\). Segments \(CM\) and \(AN\) intersect at \(G\). Find the length \(AG\).

331.

An estate of $362,880 is to be divided among three heirs, Alden, Blair, and Cary. According to the will, Alden is to get two parts, Blair three parts, and Cary four parts. What does this mean in terms of dollars and cents?

332.

What is the relationship between the length of the hypotenuse and the length of the legs in a 45°-45°-90° triangle?

333.

The area of a parallelogram can be found by multiplying the distance between two parallel sides by the length of either of those sides. Explain why this formula works.

334.

Using GeoGebra, plot the points \(A = (0, 0)\), \(B = (4, −3)\), \(C = (6, 3)\), \(P = (−2, 7)\), \(Q = (9, 5)\), and \(R = (7, 19)\). Measure the angles of \(\Delta ABC\) and \(\Delta PQR\). Create ratios of the lengths of the corresponding sides. Find justification for any conclusions you make. (If you choose not to use GeoGebra, leave all answers in simplest radical form.)

335.

(a)

The perimeter of a square is 36, what is the length of a diagonal of the square?

(b)

The area of a square is 36, what is the length of a diagonal of the square?

336.

Apply the transformation \(T (x, y) = (3x, 3y)\) to the \(\Delta PQR\) whose vertices are \(P = (3, −1)\), \(Q = (1, 2)\), and \(R = (4, 3)\). Compare the sides and angles of the image \(\Delta P'Q'R'\) with the corresponding parts of \(\Delta PQR\). This transformation is an example of a dilation.

337.

Show that the altitude drawn to the hypotenuse of any right triangle divides the triangle into two triangles that have the same angles as the original.

338.

State the relationship of the sides of a 30°-60°-90° triangle if the shortest side is \(s\).

339.

One figure is similar to another figure if the points of the first figure can be matched with the points of the second figure in such a way that corresponding distances are proportional. In other words, there is a ratio of similarity, \(k\), such that every distance on the second figure is \(k\) times the corresponding distances on the first figure.

(a)

In GeoGebra plot the points \(K = (1, −3)\), \(L = (4, 1)\), \(M = (2, 3)\), \(P = (6, 5)\), \(Q = (2, 5)\) and \(R = (7, −2)\).

(b)

Is \(\Delta KLM\) similar to \(\Delta RPQ\)? Justify with measurements from GeoGebra.

(c)

Would it be correct to say that \(\Delta MKL\) is similar to \(\Delta RQP\)?

340.

You have learned that the formula for the area of a triangle is \(A = {\textstyle{1 \over 2}}bh\). Find a formula for the area of an equilateral triangle in terms of the side, \(s\). Hint: Remember that an equilateral triangle is made up of two 30°-60°-90° triangles.

341.

Draw a right triangle that has a 15-cm hypotenuse and a 27° angle. To the nearest tenth of a cm, measure the side opposite the 27° angle, and then express your answer as a percentage of the length of the hypotenuse. Compare your answer with the value obtained from your calculator when you enter SIN(27) in degree mode.

342.

(Continuation) Repeat the process on a right triangle that has a 10-cm hypotenuse and a 65° angle. Try an example of your choosing. Write a summary of your findings.

343.

CHALLENGE: In \(\Delta ABC\), points \(M\) and \(N\) are marked on sides \(AB\) and \(AC\), respectively, so that \(AM:AB=1:3=AN:AC\). Why are segments \(MN\) and \(BC\) parallel?

344.

Create a diagram that will help you derive a formula for the area of a trapezoid. Recall that a trapezoid’s parallel sides are its bases (base₁ and base₂) and the distance between them is its height (altitude). Can you find any additional ways to demonstrate this?

345.

What is the length of an altitude of an equilateral triangle with perimeter 36?

346.

If \(\Delta ABC\) has a right angle at \(C\), the ratio \(AC:AB\) is called the sine ratio of \(\angle B\), or simply the sine of \(B\), and is usually written \(\sin B\). What should the ratio \(BC:AB\) be called? Without using your calculator, can you predict what the value of the sine ratio for a 30° angle is? How about the sine ratio for a 60° angle?

347.

If two sides of a triangle are 5 and 10, what is the range of values for the third side?

348.

Let \(C = (1, 4)\), \(P = (5, 2)\), and \(P' = (13, −2)\). There is a dilation that leaves \(C\) where it is and transforms \(P\) into \(P'\). The point \(C\) is called the dilation center. Explain why the scale factor of this dilation is 3. Keeping \(C\) as the center of dilation, calculate \(Q'\) given that \(Q = (3, 5)\). Calculate \(R\), given that \(R' = (−6, 7)\), keeping \(C\) as the center of dilation.

349.

What is the size of the acute angle formed by the x-axis and the line \(3x + 2y = 12\)?

350.

To actually draw a right triangle that has a 1° angle and measure its sides accurately is difficult. To get the sine ratio for a 1° angle, however, there is an easy way – just use your calculator. Is the ratio a small or large number? How large can a sine ratio be?