251.

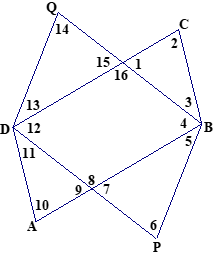
In the figure below, it is given that \(ABCD\) and \(PBQD\) are parallelograms. Which of the numbered angles must be the same size as the angle numbered 1? Give a reason for each angle.

252.

\(\Delta PQR\) has a right angle at \(P\). Let \(M\) be the midpoint of \(QR\) and let \(F\) be the point where the altitude through \(P\) meets \(QR\). Given that \(\angle FPM\) is 18°, find the sizes of \(\angle Q\) and \(\angle R\).

253.

Given that \(ABCDEFG\)… is a regular \(n\)-sided polygon, with \(\angle CAB = 12^\circ \), find \(n\).

254.

Midsegment Theorem: State the properties of the segment that connects the midpoints of two sides of a triangle. A triangle is created by placing with vertices at points \((0,0)\), \((7,4)\) and \((1,3)\). What are the coordinates of the endpoints of a midsegment of this triangle?

255.

Draw \(\Delta ABC\) so that \(\angle A\) and \(\angle B\) are both 42°. Why should \(AB\) be longer than \(BC\)? Extend \(CB\) to \(E\), so that \(CB = BE\). Mark \(D\) between \(A\) and \(B\) so that \(DB = BC\), then draw the line \(ED\), which intersects \(AC\) at \(F\). Find the size of \(\angle CFD\).

256.

How can one tell whether a given quadrilateral is a parallelogram? In other words, how much evidence is needed to be sure of such a conclusion? Hint: There are six ways to definitively show that a quadrilateral is a parallelogram.

257.

The diagram at right shows three congruent regular pentagons that share a common vertex \(P\). The three polygons do not quite surround \(P\). Find the size of the uncovered acute angle at \(P\).

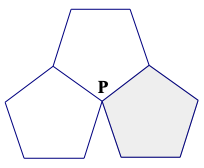
258.

(Continuation) If the shaded pentagon were removed, it could be replaced by a regular \(n\)-sided polygon that would exactly fill the remaining space. Find the value of \(n\) that makes the three polygons fit perfectly.

259.

You are given a square \(ABCD\) and midpoints \(M\) and \(N\) are marked on \(BC\) and \(CD\), respectively. Draw \(AM\) and \(BN\), which meet at \(Q\). Find the size of \(\angle AQB\).

260.

Mark \(Y\) inside regular pentagon \(PQRST\), so that \(\Delta PQY\) is equilateral. Is \(\angle RYT\) straight? Explain.

261.

Suppose that \(\Delta ABC\) has a right angle at \(B\), that \(BF\) is the altitude drawn from \(B\) to \(AC\), and that \(BN\) is the median drawn from \(B\) to \(AC\). Find \(\angle ANB\) and \(\angle NBF\), given that \(\angle C\) is 42°. It will help to draw a diagram close to scale.

262.

The midpoints of the sides of a triangle are \(M = (3, −1)\), \(N = (4, 3)\), and \(P = (0, 5)\). Find coordinates for the vertices of the triangle.

263.

The diagonals of a rhombus have lengths 18 and 24. How long are the sides of the rhombus?

264.

A trapezoid is a quadrilateral with exactly one pair of parallel sides. If the non-parallel sides have the same length, the trapezoid is isosceles. Make a diagram of an isosceles trapezoid whose sides have lengths 7 in., 10 in., 19 in., and 10 in. Find the altitude of this trapezoid (the distance that separates the parallel sides), then find the enclosed area.

265.

If a quadrilateral is a rectangle, then its diagonals have the same length. What is the converse of this true statement? Is the converse true? Explain.

266.

The diagonals of a parallelogram always bisect each other. Is it possible for the diagonals of a trapezoid to bisect each other? Explain.

267.

A trapezoid has a 60° angle and a 45° angle. What are the other angles?

268.

A trapezoid has a 60° angle and a 120° angle. What are the other angles?

269.

An \(n\)-sided polygon has the property that the sum of the measures of its exterior angles is equal to the sum of the measures of its interior angles. Find \(n\).

270.

Trapezoid \(ABCD\) has parallel sides \(AB\) and \(CD\), a right angle at \(D\), and the lengths \(AB = 15\), \(BC = 10\), and \(CD = 7\). Find the length \(DA\).

271.

In the diagram below, \(\Delta AGB\) is an equilateral triangle, \(\overline {AN} \) is the side of a square. \(\overline {AD} \) is the side of a regular pentagon, \(\overline {AJ} \) is the side of a regular hexagon, and \(\overline {AR} \) is the side of a regular octagon. \(\overline {AB} \) is a side shared by all of the regular polygons. Find:

1. \(\angle GAF\)
2. \(\angle NAR\)
3. \(\angle JAF\)
4. \(\angle GAJ\)

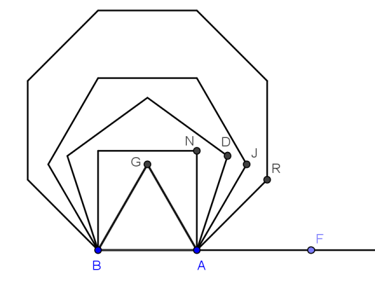
272.

A line of positive slope is drawn so that it makes a 60° angle where it intersects the x-axis. What is the slope of this line?

273.

What can be said about quadrilateral \(ABCD\) if it has supplementary consecutive angles?

274.

If \(MNPQRSTUV\) is a regular polygon, then how large is each of its interior angles? If \(MN\) and \(QP\) are extended to meet at \(A\) then how large is \(\angle PAN\)?

275.

Is it possible for the side lengths of a triangle to be 23, 19, and 44? Explain.

276.

Suppose that \(ABCD\) is a square with \(AB = 6\). Let \(N\) be the midpoint of \(CD\) and \(F\) be the intersection of \(AN\) and \(BD\). What is the length of \(AF\)? Hint: Look at \(\Delta ADC\) and think about what is special about point \(F\).

277.

The parallel sides of trapezoid \(ABCD\) are \(AD\) and \(BC\). Given that sides \(AB\), \(BC\), and \(CD\) are each half as long as side \(AD\), find the size of \(\angle D\).

278.

The altitudes of an equilateral triangle all have length 12 cm. How long are its sides?

279.

Given a triangle, you have found the following result: The point where two medians intersect (the centroid) is twice as far from one end of a median as it is from the other end of the same median. Improve the statement of the preceding theorem so that the reader knows which end of the median is which.

280.

Let \(ABCD\) be a parallelogram, with \(M\) the midpoint of \(DA\), and diagonal \(AC\) of length 36. Let \(G\) be the intersection of \(MB\) and \(AC\) and draw in diagonal \(DB\). What is the length of \(AG\)?

281.

The diagonals of a square have length 10. How long are the sides of the square?

282.

\(\Delta PQR\) is isosceles, with \(PQ = 13 = PR\) and \(QR = 10\). Find the distance from \(P\) to the centroid of \(\Delta PQR\). Find the distance from \(Q\) to the centroid of \(\Delta PQR\).

283.

In \(\Delta ABC\), let \(M\) be the midpoint of \(AB\) and \(N\) be the midpoint of \(AC\). Suppose that you measure \(MN\) and find it to be 7.3 cm long. How long would \(BC\) be, if you measured it? If you were to measure \(\angle AMN\) and \(\angle ABC\), what would you find?

284.

Justify the following Venn diagram.

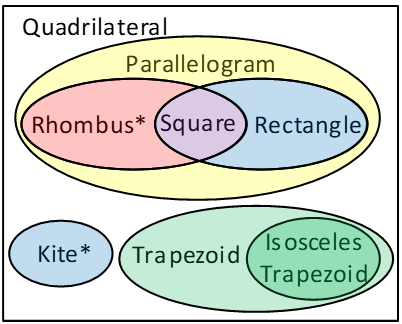
* When all four sides of a kite are the same length, a kite satisfies the definition of a rhombus.

285.

Check the properties that each type of quadrilateral holds. The columns are parallelogram, rectangle, rhombus, square, kite, trapezoid, and isosceles trapezoid.

Property	Par.	Rect.	Rhom.	Sq.	Kite	Trap.	IsosTrap
a) Opposite sides are parallel
b) Opposite sides are congruent
c) Exactly one pair of opposite sides is parallel
d) Opposite angles are congruent
e) Exactly one pair of angles is congruent
f) Consecutive angles are supplementary
g) Base angles are congruent
h) Diagonals bisect each other
i) Diagonals are congruent
j) Diagonals are perpendicular
k) Diagonals bisect opposite angles
l) Exactly one diagonal is the perpendicular bisector of the other

286.

In \(\Delta SUN\), let \(P\) be the midpoint of segment \(SU\) and let \(Q \) be the midpoint of segment \(SN\). Draw the line through \(P\) parallel to segment \(SN\) and the line through \(Q\) parallel to segment \(SU\); these lines intersect at \(J\). What can you say about the location of point \(J\)?

287.

A pendulum hangs from a hook attached to the ceiling of a room. The hook is four feet away from the nearest wall and the pendulum just touches the floor. If you swing the pendulum, the bottom of the pendulum hits a point on the wall that is three inches above the floor. How high is the ceiling? Make a clear diagram for this problem!

288.

A triangle with sides of 5, 12, and 13 must be a right triangle. Keeping the legs constant, how would the triangle change if the hypotenuse was lengthened to 15? 17? 19?

289.

(Continuation) What can be said about a triangle if the sum of the squares of the two shorter sides is smaller than the square of the longest side?

290.

What if the hypotenuse of a 5-12-13 triangle was shortened to 12? 7? 5?

291.

(Continuation) What can be said about a triangle if the sum of the squares of the two shorter sides is larger than the square of the longest side?

292.

In the diagram below, the octagon is regular. Find the measures of the angles labeled a, b, c, and d.

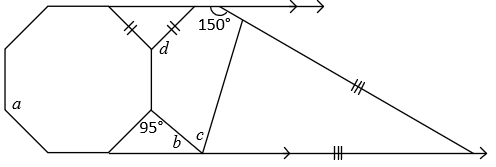
293.

Mark \(A = (0, 0)\) and \(B = (10, 0)\) on your graph paper, and use your protractor to draw the line of positive slope through \(A\) that makes a 25° angle with \(AB\). Calculate (approximately) the slope of this line by making suitable measurements.

294.

(Continuation) Set your calculator to Degree mode. On a TI-84, press the MODE button, and select the Degree option for angles. On a NumWorks calculator go to Settings. Return to the home screen, and press the TAN button to enter the expression TAN(25), then press ENTER. You should see that the display agrees with your answer to the preceding item.

295.

How does the value of the tangent of an angle change as an angle increases from 0 to 90°? Is there a direct relationship between the slope and the angle measure?

296.

A line drawn parallel to the side \(BC\) of \(\Delta ABC\) intersects side \(AB\) at \(P\) and side \(AC\) at \(Q\). The measurements \(AP = 3.8\)in, \(PB = 7.6\)in, and \(AQ = 5.6\)in are made. If segment \(QC\) were now measured, how long would it be?

297 - 301

Below is a list of true statements. Use this list to answer questions 297 - 301.

1. If a quadrilateral has two pairs of parallel sides, then its diagonals bisect each other.
2. If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral must be a parallelogram.
3. If both pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.
4. If a quadrilateral has two pairs of equal adjacent sides, then its diagonals are perpendicular.
5. If one of the medians of a triangle is half the length of the side to which it is drawn, then the triangle is a right triangle.
6. If a segment joins two of the midpoints of the sides of a triangle, then is parallel to the third side, and is half the length of the third side.
7. Both pairs of opposite sides of a parallelogram are congruent.
8. The sum of the exterior angles of any polygon – one at each vertex – is 360°.
9. The median drawn to the hypotenuse of a right triangle is half the length of the hypotenuse.
   
10. If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
11. Both pairs of opposite angles of a parallelogram are congruent.
12. The medians of any triangle are concurrent at a point that is two thirds of the way from any vertex to the midpoint of the opposite side.

297.

Find the four three pairs of statements whose converses are also in the list.

298.

Find the statement whose converse is false.

299.

Find the Sentry Theorem.

300.

Find the Midsegment Theorem.

301.

Find the Centroid Theorem.