201.

Given that \((−1, 4)\) is the reflected image of \((5, 2)\), find an equation for the line of reflection.

202.

Point \((0, 1)\) is reflected across the line \(2x + 3y = 6\). Find coordinates for its image.

203.

The converse of a statement of the form “If \(A\) then \(B\)” is the statement “If \(B\) then \(A\).” Write the converse of the statement “If it is Tuesday, we have morning reports after first period”

204.

(Continuation) “If point \(P\) is equidistant from the coordinate axes, then point \(P\) is on the line \(y = x\)”.

1. Write the converse of the given statement. Is it true?
2. Give an example of a true statement whose converse is false.
3. Give an example of a true statement whose converse is also true.

205.

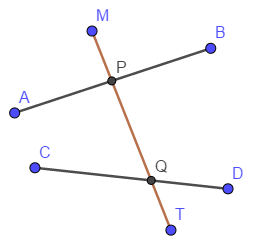
The diagram below shows lines \(AB\) and \(CD\) intersected by line \(MT\), which is called a transversal. There are two groups of angles: one group of four angles with vertex at \(P\), and another group with vertex at \(Q\). There is special terminology to describe pairs of angles – one from each group. If the angles are on different sides of the transversal, they are called alternate, for example, \(\angle APM\) and \(\angle PQD\). \(\angle BPQ\) is an interior angle because it is between the lines \(AB\) and \(CD\), and \(\angle CQT\) is exterior. Thus, angles \(\angle APQ\) and \(\angle PQD\) are called alternate interior, while \(\angle MPB\) and \(\angle CQT\) are called alternate exterior. \(\angle APQ\) and \(\angle PQC\) are called same side interior angles. On the other hand, the pair of angles \(\angle MPB\) and \(\angle PQD\) – which are non-alternate angles, one interior, and the other exterior – is called corresponding. Refer to the diagram and name

1. the other pair of alternate interior angles;
2. the other pair of alternate exterior angles;
3. the other pair of same side interior angles;
4. the angles that correspond to \(\angle CQT\) and to \(\angle TQD\).

206.

Let \(P = (2, 7)\), \(B = (6, 11)\), and \(M = (5, 2)\). Find a point \(D\) that makes \(\overrightarrow{PB} = \overrightarrow{DM}\). What can you say about quadrilateral \(PBMD\)?

207.

The diagonals of quadrilateral \(ABCD\) intersect perpendicularly at \(O\). What can be said about quadrilateral \(ABCD\)?

208.

What do you call (a) an equiangular quadrilateral? (b) an equilateral quadrilateral? (c) a regular quadrilateral?

209.

In quadrilateral \(ABCD\), it is given that vectors \(\overrightarrow {AB} = \overrightarrow {DC} \). What kind of a quadrilateral is \(ABCD\)? What can be said about the vectors \(\overrightarrow {AD} \) and \(\overrightarrow {BC} \)?

210.

Find the area of a triangle formed by placing the vectors \([3, 6]\) and \([7, 1]\) tail-to-tail.

211.

(Continuation) Find the length of the longest altitude of your triangle.

Spreadsheet Lab #4: Image of a Point Reflected Across a Line (not for spring 2022)

212.

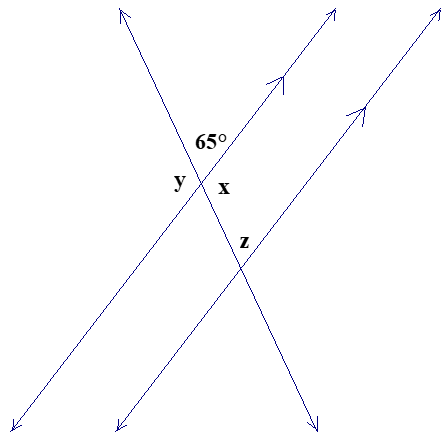
For the diagram below, find the measure of the angles indicated. Notice the custom of marking arrows on lines to indicate that they are known to be parallel.

213.

It is a postulate (assumed without proof) that given two parallel lines cut by a transversal, corresponding angles are congruent. Given two parallel lines cut by a transversal, prove that a pair of alternate interior angles is congruent.

214.

Asked to reflect the point \(P = (4, 0)\) across the mirror line \(y = 2x\), Aubrey reasoned this way: First mark the point \(A = (1, 2)\) on the line, then use the vector \([−3, 2]\) from \(P\) to \(A\) to reach from \(A\) to \(P' = (−2, 4)\), which is the requested image. What did Aubrey do wrong? Explain and find out where \(P'\) should be.

215.

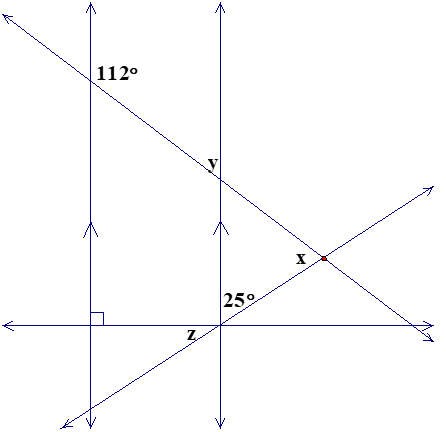
For the diagram below, find the measure of the angles indicated.

216.

Given isosceles \(\Delta ABC\) where \(AB = BC =10\) and the altitude from \(B\) has length 4. Find the length of the base. Leave your answer in simplest radical form.

217.

You probably know that the sum of the angles of a triangle is a straight angle. One way to confirm this is to draw a line through one of the vertices, parallel to the opposite side. This creates some alternate interior angles. Finish the demonstration.

218.

If it is known that one pair of alternate interior angles are congruent, what can be said about

1. the other pair of alternate interior angles?
2. either pair of alternate exterior angles?
3. any pair of corresponding angles?
4. either pair of same side interior angles?

219.

Suppose that \(ABCD\) is a square and that \(\Delta CDP\) is an equilateral triangle, with \(P\) outside the square. What is the size of \(\angle PAD\)?

220.

Recall that a quadrilateral that has two pairs of parallel opposite sides is called a parallelogram. What can be said about the angles of such a figure? Consider both the opposite angles and the consecutive angles.

221.

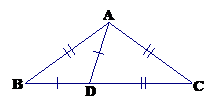
In the figure below, it is given that \(BDC\) is straight, \(BD = DA\), and \(AB = AC = DC\). Find the size of \(\angle C\).

222.

Given an arbitrary triangle, what can you say about the sum of the three exterior angles, one for each vertex of the triangle?

223.

In the diagrams below, the goal is to find the sizes of the angles marked with letters, using the given numerical information.

(a)

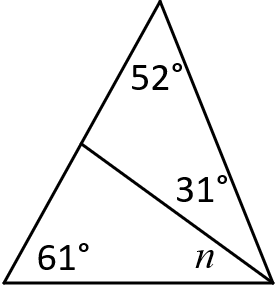
(b)

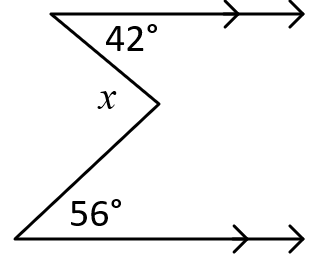
(c)

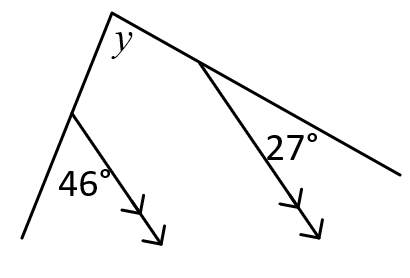
224.

Prove that the sum of the angles of any quadrilateral is 360°.

225.

Write the Pythagorean Theorem in if…then form. State the converse of the Pythagorean Theorem.

226.

Fill in the table.

Number of sides of the polygon	3	4	5	6	7	8	\(n\)
Number of non-overlapping triangles that you can divide the polygon into.	1	2
Sum of the interior angles of the polygon	180°	360°
One angle in a regular \(n\)-sided polygon

227.

Given parallelogram \(PQRS\), let \(T\) be the intersection of the bisectors of \(\angle P\) and \(\angle Q\). Without knowing the sizes of the angles of \(PQRS\), calculate the size of \(\angle PTQ\). Recall that the diagonals of a parallelogram are not necessarily the angle bisectors.

228.

In the figures below, find the sizes of the angles indicated by letters:

(a)

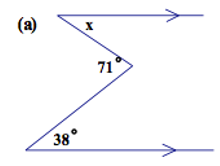
(b)

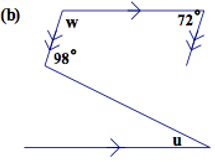
229.

Mark the point \(P\) inside square \(ABCD\) that makes \(\Delta CDP\) equilateral. Calculate the size of \(\angle PAD\).

230.

If a quadrilateral is a parallelogram, then both pairs of opposite angles are congruent. What is the converse of this statement? Is the converse true?

231.

Find the measure of an interior angle of a regular decagon.

232.

If \(\Delta ABC\) is any triangle, and \(\angle {TAC}\) is one of its exterior angles, then what can be said about the size of \(\angle TAC\), in relation to the other angles of the figure?

233.

In regular pentagon \(ABCDE\), draw diagonal \(AC\). What are the sizes of the angles of \(\Delta ABC\)? Prove that segments \(AC\) and \(DE\) are parallel.

234.

Given square \(ABCD\), let \(P\) and \(Q\) be the points outside the square that make \(\Delta CDP\) and \(\Delta BCQ\) equilateral. Prove that \(\Delta APQ\) is also equilateral.

235.

The sides of an equilateral triangle are 12 cm long. How long is an altitude of this triangle? What are the angles of a right triangle created by drawing an altitude? How does the short side of this right triangle compare with the other two sides? Please leave your lengths in simplest radical form.

236.

If a quadrilateral is a parallelogram, then both pairs of opposite sides are congruent. Explain. What is the converse of this statement? Is it true?

237.

In \(\Delta ABC\), it is given that \(\angle A\) is 59° and \(\angle B\) is 53°. The altitude from \(B\) to line \(AC\) is extended until it intersects the line through \(A\) that is parallel to segment \(BC\); they meet at \(K\). Calculate the size of \(\angle AKB.\)

238.

Tate walks along the boundary of a four-sided plot of land, writing down the number of degrees turned at each corner. What is the sum of these four numbers?

239.

If the diagonals of a quadrilateral bisect each other, then the figure is a parallelogram. Prove that this is so. What about the converse statement?

240.

CHALLENGE: In the figure at below, there are two \(x\)-degree angles, and four of the segments are congruent as marked. Find \(x\).

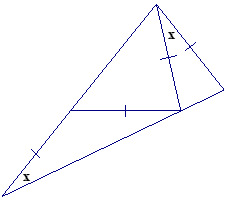
241.

Xiaodan walks along the boundary of a five-sided plot of land, writing down the number of degrees that she turns at each corner. What is the sum of these five numbers?

242.

Lillian walks along the boundary of a seventy-sided plot of land, writing down the number of degrees that she turns at each corner. What is the sum of these seventy numbers?

243.

The preceding two questions illustrate the Sentry Theorem. What does this theorem say, and why has it been given this name?

244.

A rectangle with area 540 has one side of length 15. Find the length of the other side and the diagonals.

245.

A right triangle has a 24-cm perimeter and its hypotenuse is twice as long as its shorter leg. To the nearest hundredth of a cm, find the lengths of all three sides of this triangle.

246.

Suppose that quadrilateral \(ABCD\) has the property that \(AB\) and \(CD\) are congruent and parallel. Is this enough information to prove that \(ABCD\) is a parallelogram? Explain.

Spreadsheet Lab #5: Angles in Regular Polygons

247.

The midsegment of a triangle is a segment that connects the midpoints of two sides of the triangle. Given a triangle with coordinates \(A = \left( {1,7} \right)\), \(B = \left( {5,3} \right)\) and \(C = \left( { - 1,1} \right)\) find the segment that connects the midpoints of sides \(AB\) and \(AC\), label the midpoints \(M\) and \(N\), respectively.

(a)

Find the length of the midsegment \(MN\) and compare it to the length of \(BC\).

(b)

What can be said about the lines containing segments \(BC\) and \(MN\)?

248.

A regular, \(n\)-sided polygon has 18° exterior angles. Find the integer \(n\).

249.

Draw a \(\Delta ABC\), and let \(AM\) and \(BN\) be two of its medians, which intersect at \(G\). Extend \(AM\) to the point \(P\) that makes \(GM = MP\). Prove that \(PBGC\) is a parallelogram.

250.

\(\Delta EWS\) has a perimeter of 26 and \(SE = {\textstyle{1 \over 2}}WE\). The length of the midsegment parallel to \(WS\) is 4. Find the lengths of the three sides of this triangle.