151.

In quadrilateral \(ABCD\), it is given that \(AB = CD\) and \(BC = DA\). Prove that angles \(\angle ACD\) and \(\angle CAB\) are the same size. Note: If a polygon has more than three vertices, the labeling convention is to place the letters around the polygon in the order that they are listed. Thus, \(AC\) should be one of the diagonals of \(ABCD\).

152.

Find the area of the triangle defined by \(E = (−2, 8)\), \(W = (11, 2)\), and \(S = (−2, −4)\). Now, find the area of \(\Delta WLS\) where \(L\) is \((−2, 0)\).

153.

A segment from one of the vertices of a triangle to the midpoint of the opposite side is called a median. Consider the triangle defined by \(A = (−2, 0)\), \(B = (6, 0)\), and \(C = (4, 6)\).

1. Find an equation for the line that contains the median drawn from \(A\) to \(BC\).
2. Find an equation for the line that contains the median drawn from \(B\) to \(AC\).
3. Find coordinates for \(G\), the intersection of the medians from \(A\) and \(B\).
4. Let \(M\) be the midpoint of \(AB\). Determine whether or not \(M\), \(G\), and \(C\) are collinear.

154.

The line \(3x + 2y = 16\) is the perpendicular bisector of the segment \(AB\). Find coordinates of point \(B\) given that

1. \(A = (−1, 3)\)
2. \(A = (0, 3)\)

155.

(Continuation) Point \(B\) is called the reflection of \(A\) across the line \(3x + 2y = 16\); sometimes \(B\) is simply called the image of \(A\). Explain this terminology. Using the same line, find another point \(C\) and its image \(C'\). Explain your method for finding your pair of points.

156.

A rhombus has 25-cm sides, and one diagonal is 14 cm long. How long is the other diagonal?

157.

Let \(A = (0, 0)\) and \(B = (12, 5)\), and let \(C\) be the point on segment \(AB\) that is 8 units from \(A\). Find coordinates for \(C\).

158.

Prove that one of the diagonals of a kite is bisected by the other.

159.

Let \(A = (1, 4)\), \(B = (8, 0)\), and \(C = (7, 8)\). Find the area of \(\Delta ABC\).

160.

Sketch \(\Delta PQR\), where \(P = (1, 1)\), \(Q = (1, 3)\), and \(R = (4, 1)\). For each of the following, apply the given transformation \(T\) to the vertices of \(\Delta PQR\), sketch the image \(\Delta P'Q'R'\). It is advisable to sketch the respective images in different colors from the original \(\Delta PQR\). Then decide which of the terms reflection, rotation, translation, or glide-reflection accurately describes the action of \(T\). Provide appropriate detail to justify your choices.

1. \(T (x, y) = (x + 3, y - 2)\)
2. \(T (x, y) = (y, x)\)
3. \(T (x, y) = (-x + 2, -y + 4)\)
4. \(T (x, y) = (x + 3, - y)\)

161.

Robin is mowing a rectangular field that measures 24 yards by 32 yards, by pushing the mower around and around the outside of the plot. This creates a widening border that surrounds the un-mowed grass in the center. During a brief rest, Robin wonders whether the job is half done yet. How wide is the uniform mowed border when Robin is half done?

162.

\(\Delta ABC\) is isosceles, with \(AB = BC\), and \(\angle BAC\) is 56°. Find the remaining two angles of this triangle.

163.

Terry walked 1 mile due north, 2 miles due east, then 3 miles due north again and then once more east for 4 miles. How far is Terry from their starting point?

164.

\(\Delta ABC\) is isosceles, with \(AB = BC\), and \(\angle ABC\) is 56°. Find the remaining two angles of this triangle.

165.

Find the area of the triangle whose vertices are \(A = (−2, 3)\), \(B = (6, 7)\), and \(C = (0, 6)\).

166.

Let \(A = (−4, 0)\), \(B = (0, 6)\), and \(C = (6, 0)\).

1. Find equations for the three lines that contain the altitudes of \(\Delta ABC\).
2. Show that the three altitudes are concurrent, by finding coordinates for their common point. The point of concurrence is called the orthocenter of \(\Delta ABC\).

167.

Pat and Chris were out in their rowboat one day, and Chris spied a water lily. Knowing that Pat liked a mathematical challenge, Chris announced that, with the help of the plant, it was possible to calculate the depth of the water under the boat. When pulled taut, directly over its root, the top of the plant was originally 10 inches above the water surface. While Pat held the top of the plant, which remained rooted to the lake bottom, Chris gently rowed the boat five feet. This forced Pat’s hand to the water surface. Use this information to calculate the depth of the water.

168.

Prove that if \(\Delta ABC\) is isosceles, with \(AB = AC\), then the medians drawn from vertices \(B\) and \(C\) must have the same length.

169.

CHALLENGE: Find \(k\) so that the vectors \([4, −3]\) and \([k, −6]\)

1. point in the same direction
2. are perpendicular.

170.

Let \(A = (−4, 0)\), \(B = (0, 6)\), and \(C = (6, 0)\).

1. Find equations for the three medians of \(\Delta ABC\).
2. Show that the three medians are concurrent, by finding coordinates for their common point. The point of concurrence is called the centroid of \(\Delta ABC\).

171.

Given points \(A = (0, 0)\) and \(B = (−2, 7)\), find coordinates for \(C\) and \(D\) so that \(ABCD\) is a square.

172.

CHALLENGE: Let \(A = (0, 12)\) and \(B = (25, 12)\). If possible, find coordinates for a point \(P\) on the x-axis that makes \(\angle APB\) a right angle

173.

The lines \(3x + 4y = 12\) and \(3x + 4y = 72\) are parallel. Explain why, and then find the distance that separates these lines. You will have to decide what “distance” means in this context.

174.

Give an example of an equiangular polygon that is not equilateral.

175.

On a separate sheet of paper, draw parallelogram \(PQRS\) with vertices at \(P = (1, 1)\), \(Q = (4, 6)\), \(R = (10, 6)\), and \(S = (7, 1)\). Cut out your parallelogram and dissect it to form a rectangle. What can you conclude about the area of a parallelogram?

176.

Prove that a diagonal of a square divides it into two congruent triangles.

177.

Find the area of the parallelogram whose vertices are \((0, 0)\), \((7, 2)\), \((8, 5)\), and \((1, 3)\).

178.

Given the points \(A = (0, 0)\), \(B = (7, 1)\), and \(D = (3, 4)\), find coordinates for the point \(C\) that makes quadrilateral \(ABCD\) a parallelogram. What if the question had requested \(ABDC\) instead?

179.

Find a vector that is perpendicular to the line \(3x − 4y = 6\).

180.

Let \(P = (−1, 3)\). Find the point \(Q\) for which the line \(2x + y = 5\) serves as the perpendicular bisector of segment \(PQ\).

181.

Find points on the line \(3x + 5y = 15\) that are equidistant from the coordinate axes.

182.

Plot all points that are 3 units from the x-axis. Describe the configuration. Then, plot all the points 3 units from \((5, 4)\) and describe their configuration.

183.

In \(\Delta ABC\), it is given that \(CA = CB\). Points \(P\) and \(Q\) are marked on segments \(CA\) and \(CB\), respectively, so that angles \(\angle CBP\) and \(\angle CAQ\) are the same size. Prove that \(CP = CQ\).

184.

Let \(A = (3, 4)\), \(B = (0, −5)\), and \(C = (4, −3)\). Find equations for the perpendicular bisectors of segments \(AB\) and \(BC\), and coordinates for their common point \(K\). Calculate lengths \(KA\), \(KB\), and \(KC\). Why is \(K\) also on the perpendicular bisector of segment \(CA\)?

185.

(Continuation) A circle centered at \(K\) can be drawn so that it goes through all three vertices of \(\Delta ABC\). Explain. This is why \(K\) is called the circumcenter of the triangle. In general, how do you locate the circumcenter of a triangle?

186.

CHALLENGE: The figure at right shows a parallelogram \(PQRS\), three of whose vertices are \(P = (0, 0)\), \(Q = (a, b)\), and \(S = (c, d)\). You can also see that \(TRUP\) is a rectangle. All your expressions should be in terms of \(a\), \(b\), \(c\), and \(d\).

1. Find the coordinates of \(R\).
2. Write an expression for the area of the rectangle \(TRUP\).
3. Find expressions for the areas of triangles \(TSR\), \(TSP\), \(PQU\), and \(RQU\).
4. Find an expression for the area of \(PQRS\) and simplify your formula.
5. There are two limitations on this formula. What do you think they are?

Spreadsheet Lab #3: (not for Spring 2022) Perpendicular Bisector, Altitude, and Median

187.

Some Terminology: Draw a parallelogram whose adjacent edges are determined by vectors \([2, 5]\) and \([7, −1]\), placed so that they have a common initial point. This is called placing vectors tail-to-tail. Find the area of the parallelogram.

188.

A polygon that is both equilateral and equiangular is called regular. Prove that all diagonals of a regular pentagon (five sides) have the same length.

189.

Solve for x: \(\sqrt{x+1}=7\)

190.

Write an equation that says that the distance from point \((x, y)\) to \((3, 5)\) is equal to the distance from the point \((x, y)\) to \((7, −1)\). Do not simplify your formula.

191.

Find the area of the parallelogram whose vertices are \((2, 5)\), \((7, 6)\), \((10, 10)\), and \((5, 9)\).

192.

Let \(E = (2, 7)\) and \(F = (10, 1)\). There are two points on line \(EF\) that are 3 units from \(E\). Use vectors to find coordinates for both of them.

193.

Find coordinates for the point equidistant from \((−1, 5)\), \((8, 2)\), and \((6, −2)\).

194.

Simplify the equation \(\sqrt {{{(x - 3)}^2} + {{(y - 5)}^2}} = \sqrt {{{(x - 7)}^2} + {{(y + 1)}^2}} \). Interpret your result.

195.

Use the diagram at right to help you explain why SSA evidence is not by itself sufficient to justify the congruence of triangles. The tick marks designate segments that have the same length.

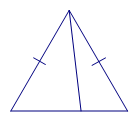
196.

(Continuation) You have recently seen that there is no generally reliable SSA criterion for congruence. If the angle part of such a correspondence is a right angle, however, the criterion is reliable. Justify this so-called hypotenuse-leg criterion (which is abbreviated HL).

197.

Find an equation for the line through point \((7, 9)\) that is perpendicular to vector \([5, −2]\).

198.

Describe a transformation that carries the triangle with vertices \((1, 2)\), \((6, 7)\), and \((10, 5)\) onto the triangle with vertices \((0, 0)\), \((7, −1)\), and \((9, 3)\). Where does your transformation send \((7, 4)\)?

199.

A triangle that has a 13-inch side, a 14-inch side, and a 15-inch side has an area of 84 square inches. Accepting this fact, find the lengths of all three altitudes of this triangle.

200.

Find the lengths of all the altitudes of the triangle whose vertices are \((0, 0)\), \((3, 0)\), and \((1, 4)\).